题目内容
已知函数f(x)是定义在R上的偶函数,且x≥0时,f(x)=(
)x,函数f(x)的值域为集合A.
(Ⅰ)求f(-1)的值;
(Ⅱ)设函数g(x)=
的定义域为集合B,若A⊆B,求实数a的取值范围.
| 1 |
| 2 |
(Ⅰ)求f(-1)的值;
(Ⅱ)设函数g(x)=
| -x2+(a-1)x+a |
分析:(Ⅰ)题目给出函数f(x)是定义在R上的偶函数,且给出x≥0时的解析式,则f(1)可求,由偶函数的性质可求f(-1)的值;
(Ⅱ)由x得范围求出f(x)的值域,由根式内部的代数式大于等于0求出定义域,再由A⊆B结合数轴可求a的取值范围.
(Ⅱ)由x得范围求出f(x)的值域,由根式内部的代数式大于等于0求出定义域,再由A⊆B结合数轴可求a的取值范围.
解答:解:(I)∵函数f(x)是定义在R上的偶函数,
∴f(-1)=f(1).
又x≥0时,f(x)=(
)x,
∴f(1)=
.
则f(-1)=
.
(II)由函数f(x)是定义在R上的偶函数,可得函数f(x)的值域A即为
x≥0时的f(x)的取值集合.
当x≥0时,0<(
)x≤1.
故函数f(x)的值域A=(0,1].
∵g(x)=
.
∴定义域B={x|-x2+(a-1)x+a≥0}.
由-x2+(a-1)x+a≥0,得
x2-(a-1)x-a≤0,
即 (x-a)(x+1)≤0.
∵A⊆B,
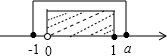
∴B=[-1,a]且a≥1.
∴实数a的取值范围是{a|a≥1}.
∴f(-1)=f(1).
又x≥0时,f(x)=(
| 1 |
| 2 |
∴f(1)=
| 1 |
| 2 |
则f(-1)=
| 1 |
| 2 |
(II)由函数f(x)是定义在R上的偶函数,可得函数f(x)的值域A即为
x≥0时的f(x)的取值集合.
当x≥0时,0<(
| 1 |
| 2 |
故函数f(x)的值域A=(0,1].
∵g(x)=
| -x2+(a-1)x+a |
∴定义域B={x|-x2+(a-1)x+a≥0}.
由-x2+(a-1)x+a≥0,得
x2-(a-1)x-a≤0,
即 (x-a)(x+1)≤0.
∵A⊆B,

∴B=[-1,a]且a≥1.
∴实数a的取值范围是{a|a≥1}.
点评:本题考查了函数的定义域及其求法,考查了集合间的关系及其应用,训练了含字母的一元二次不等式的解法,是基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+