题目内容
【题目】如图，椭圆C： 
=1（0＜b＜3）的右焦点为F，P为椭圆上一动点，连接PF交椭圆于Q点，且|PQ|的最小值为 
． 
（1）求椭圆方程；
（2）若 
，求直线PQ的方程；
（3）M，N为椭圆上关于x轴对称的两点，直线PM，PN分别与x轴交于R，S，求证：|OR||OS|为定值．
【答案】
（1）解：由题意得 
，且a=3，∴b2=4，故椭圆方程为 
（2）解：设 
与4x2+9y2=36联立，
得： 
设P（x1，y1），Q（x2，y2），则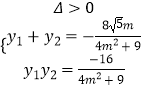 
由 
得y1=﹣2y2， 
即 
，
∴ 
（3）证明：设M（x0，y0），N（x0，﹣y0），则 
，
令y=0得 
，同理 
，
得 
，
∴|OR||OS|= 
（#）
又 
， 
∴ 
，∴ 
代入（#）
得：∴|OR||OS|=9
【解析】（1）利用椭圆的简单性质，结合已知条件求出a，b，得到椭圆方程．（2）设 与4x2+9y2=36联立，设P（x1 ， y1），Q（x2 ， y2），利用韦达定理以及判别式，通过 求出m，然后求解直线方程．（3）设M（x0 ， y0），N（x0 ， ﹣y0），则 ，令y=0得 同理 ，通过化简|OR||OS|，结合点的坐标满足椭圆方程，化简求解|OR||OS|=9．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
练习册系列答案
相关题目
