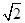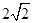题目内容
已知直线的极坐标方程为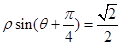
，圆
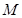的参数方程为
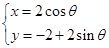（其中
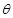为参数）.
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆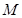上的点到直线的距离的最小值.
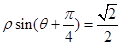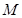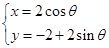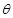，圆的参数方程为（其中为参数）.（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆
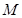上的点到直线的距离的最小值.(I)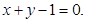
（Ⅱ）最小值为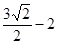
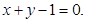（Ⅱ）最小值为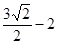(I)根据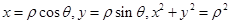
把极坐标方程化成普通方程.
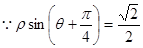111
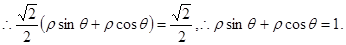
所以，该直线的直角坐标方程为：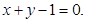
(II)化成普通方程以后，圆M上的点到直线的距离最小值等于圆心到直线的距离减去半径.
法一：圆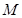的普通方程为：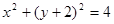
圆心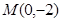
到直线
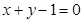的距离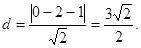
所以，圆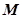
上的点到直线的距离的最小值为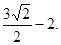
法二：直接应用圆的参数方程求解
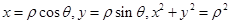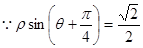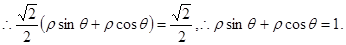
把极坐标方程化成普通方程.111所以，该直线的直角坐标方程为：
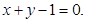
(II)化成普通方程以后，圆M上的点到直线的距离最小值等于圆心到直线的距离减去半径.
法一：圆
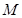的普通方程为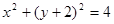：圆心
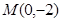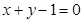到直线的距离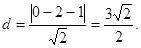所以，圆
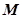上的点到直线的距离的最小值为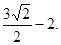法二：直接应用圆的参数方程求解
练习册系列答案
相关题目
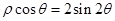表示的曲线为（ ） 
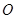为极点，以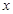
轴的正半轴为极轴建立极坐标系，已知曲线
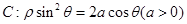，过点
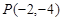的直线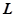
的参数方程为
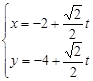，设直线
与曲线
分别交于
；
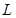的普通方程；
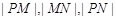成等比数列,求
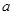的值．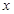
轴的正半轴为极轴建立极坐标系，已知直线
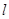的极坐标方程为
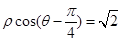，曲线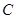
的参数方程为
（
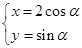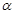为对数），求曲线
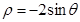的圆心的极坐标是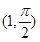
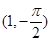
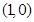
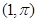
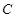的
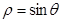，过极点
的一条直线
与圆
两点，且
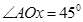，则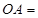
.
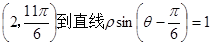的距离等于____________。
为参数r>0）,以O为极点，x轴正半轴为极轴建立极坐标系，直线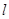
的极坐标方程为
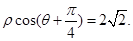若直线
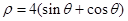和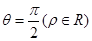
所得的弦长等于（ ）
