题目内容
由曲线y=2x2-2（1≤x≤3）及直线y=0，绕y轴旋转所得的旋转体做容器，每秒钟向容器里注水8cm3，问几秒钟后能注满容器？（坐标的长度单位是cm）分析：首先分析题目求几秒钟后水能注满容器，又已知每秒钟向容器里注水8cm3，则需要求出容器的体积，而容器是由抛物线绕对称轴旋转所得到的，可由定积分求得，即可求出结果．
解答：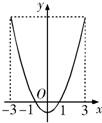
解：如图，底面是x轴上0≤x≤1部分的线段绕y轴旋转所生成的圆，
侧面是抛物线y=2x2-2上1≤x≤3，0≤y＜16部分绕y轴旋转所得的曲面．
由y=2x2-2，得x2=
，
注满容器时的体积为V=π
dy=π(
+y
=80π(cm3)．
每秒注水88cm3，充满容器所需时间为80π÷8=10π（秒）．
所以10π秒钟后能注满容器．
解：如图，底面是x轴上0≤x≤1部分的线段绕y轴旋转所生成的圆，侧面是抛物线y=2x2-2上1≤x≤3，0≤y＜16部分绕y轴旋转所得的曲面．
由y=2x2-2，得x2=
| y+2 |
| 2 |
注满容器时的体积为V=π
| ∫ | 16 0 |
| y+2 |
| 2 |
| y2 |
| 4 |
| ) | 16 0 |
每秒注水88cm3，充满容器所需时间为80π÷8=10π（秒）．
所以10π秒钟后能注满容器．
点评：此题主要考查由定积分求体积的公式的应用，其中涉及到对旋转体的理解，有一定的计算量属于中档题．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目