题目内容
【题目】若对任意的![]() ,存在实数
,存在实数![]() ,使
,使![]() 恒成立,则实数
恒成立,则实数![]() 的最大值为__________.
的最大值为__________.
【答案】9
【解析】分析:对任意的x∈[1,5],存在实数a,使![]() 恒成立,
恒成立,![]() .令f(x)=
.令f(x)=![]() +a,x∈[1,4].(b>0).f′(x)=1﹣
+a,x∈[1,4].(b>0).f′(x)=1﹣![]() =
=![]() =
=![]() .对b分类讨论,利用导数研究函数的单调性极值与最值即可得出.
.对b分类讨论,利用导数研究函数的单调性极值与最值即可得出.
详解:对任意的![]() ,存在实数
,存在实数![]() ,使
,使![]() 恒成立,
恒成立,
即![]()
令f(x)=![]() +a,x∈[1,4].(b>0).
+a,x∈[1,4].(b>0).
f′(x)=1﹣![]() =
=![]() =
=![]() .
.
对b分类讨论:
![]() ≥4时,函数f(x)在x∈[1,4]上单调递减:f(1)=1+a+b
≥4时,函数f(x)在x∈[1,4]上单调递减:f(1)=1+a+b![]() ,f(4)=4+
,f(4)=4+![]() +a
+a![]() ,即
,即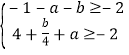 ,解得
,解得![]() ,舍去.
,舍去.
1<![]() <4时,函数f(x)在x∈[1,
<4时,函数f(x)在x∈[1,![]() )上单调递减,在(
)上单调递减,在(![]() ,4]上单调递增.f(
,4]上单调递增.f(![]() )=2
)=2![]() +a=﹣2,f(4)=4+
+a=﹣2,f(4)=4+![]() +a≤2,f(1)=1+a+b≤2,
+a≤2,f(1)=1+a+b≤2,
其中必有一个取等号,解得b=9,a=﹣8.
0<![]() ≤1时,不必要考虑.
≤1时,不必要考虑.
综上可得:b的最大值为9.
故答案为:9.

练习册系列答案
相关题目