题目内容
(本小题满分12分)
已知各项均为正数的数列 的前n项和
的前n项和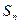 满足
满足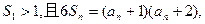
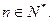
(1)求数列 的通项公式;
的通项公式;
(2)设数列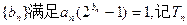 为数列
为数列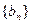 的前n项和,求证:
的前n项和,求证:
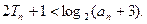
已知各项均为正数的数列
 的前n项和
的前n项和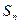 满足
满足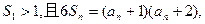
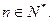
(1)求数列
 的通项公式;
的通项公式;(2)设数列
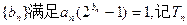 为数列
为数列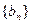 的前n项和,求证:
的前n项和,求证: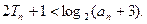
(1)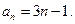
(2)证明见解析。
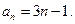
(2)证明见解析。
(1)当n=1时,有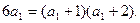
解得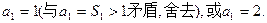 …………1分
…………1分
当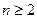 时,有
时,有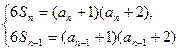 两式相减得
两式相减得
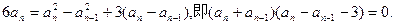 …………3分
…………3分
由题设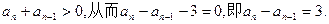
故数列 是首项为2,公差为3的等差数列
是首项为2,公差为3的等差数列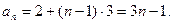 ……5分
……5分
(2)由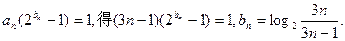 …………6分
…………6分
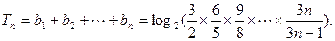
而
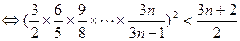
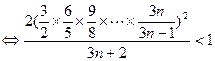 …………8分
…………8分
令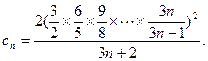
则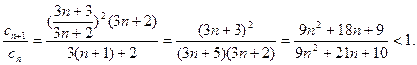
而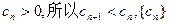 是单调递减数列.…………10分
是单调递减数列.…………10分
所以,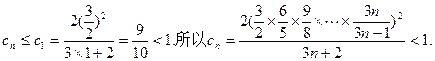
从而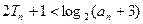 成立. …………12分
成立. …………12分
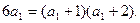
解得
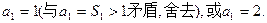 …………1分
…………1分当
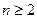 时,有
时,有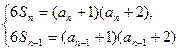 两式相减得
两式相减得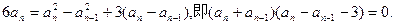 …………3分
…………3分由题设
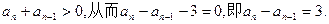
故数列
 是首项为2,公差为3的等差数列
是首项为2,公差为3的等差数列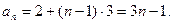 ……5分
……5分(2)由
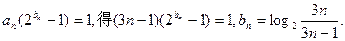 …………6分
…………6分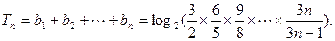
而

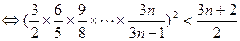
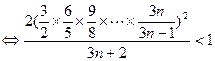 …………8分
…………8分令
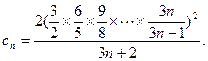
则
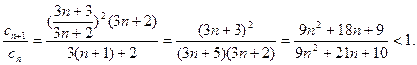
而
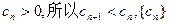 是单调递减数列.…………10分
是单调递减数列.…………10分所以,
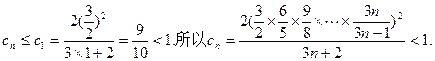
从而
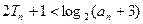 成立. …………12分
成立. …………12分
练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
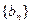 是等比数列;
是等比数列; 的通项公式;
的通项公式; ,证明数列{|
,证明数列{|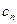 |}的前n项和Sn满足Sn<1.
|}的前n项和Sn满足Sn<1.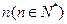 个圆盘依其半径大小,大的在下,小的在上套在
个圆盘依其半径大小,大的在下,小的在上套在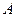 柱上,现要将套在
柱上,现要将套在 柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子
柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子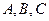 可供使用.
可供使用.
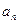 表示将
表示将 个圆盘全部从
个圆盘全部从 柱上移到
柱上移到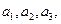 并求出
并求出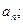 (2)记
(2)记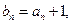 求和
求和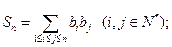
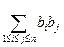 表示所有的积
表示所有的积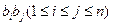 的和)
的和)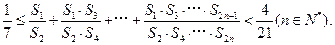
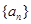 中,
中,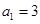 且对于任意大于
且对于任意大于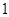 的正整数
的正整数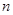 ,点
,点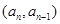 在直线
在直线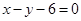 上,则
上,则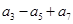 的值为( ).
的值为( ).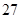
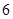
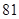
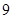
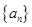 中,公差为
中,公差为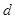 ,且
,且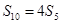 ,则
,则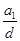 等于
等于 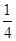
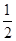
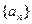 为等差数列,且
为等差数列,且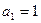 .
.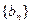 为等比数列,数列
为等比数列,数列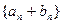 的前三项依次为3,7,13。求
的前三项依次为3,7,13。求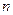 项和
项和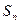 。
。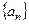 的前
的前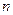 项和
项和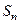 满足
满足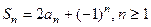 .
.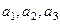 ;
;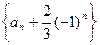 为等比数列,并求出
为等比数列,并求出