题目内容
定义在 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 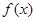 在
在 上是减函数,在
上是减函数,在 上是增函数;②
上是增函数;②  是偶函数;③
是偶函数;③ 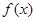 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求函数 的解析式;
的解析式;
(2)设 ,若存在
,若存在 ,使
,使 ,求实数
,求实数 的取值范围.
的取值范围.
【答案】
(1)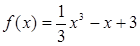 ;(2)
;(2)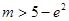 .
.
【解析】(1)要确定a,b,c的值,关键是建立关于a,b,c的三个方程.一是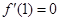 ,二是
,二是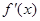 是偶函数;三是
是偶函数;三是 .
.
(2)令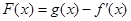 ,本题可转化为
,本题可转化为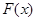 在
在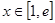 上的最小值小于零即可.
上的最小值小于零即可.
解:(I)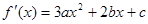 ,
,
∵ 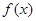 在
在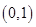 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,
∴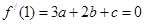 , (
, (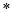 )
)
由 是偶函数得:
是偶函数得: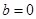 ,
,
又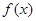 在
在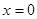 处的切线与直线
处的切线与直线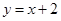 垂直,
垂直,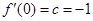 ,
,
代入(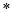 )得:
)得: 即
即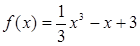 . 5分
. 5分
(II)由已知得:若存在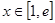 ,使
,使 ,即存在
,即存在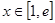 ,使
,使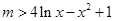 .
.
设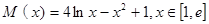 ,
,
则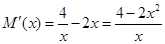 ,
,
令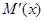 =0,∵
=0,∵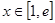 ,∴
,∴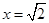 ,
,
当 时,
时,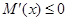 ,∴
,∴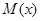 在
在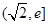 上为减函数,
上为减函数,
当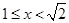 时,
时,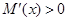 ,∴
,∴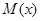 在
在 上为增函数,
上为增函数,
∴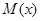 在
在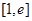 上有最大值.
上有最大值.
又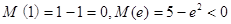 ,∴
,∴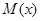 最小值为
最小值为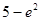 .
.
于是有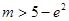 为所求. 12分
为所求. 12分

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目










 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在
在 上是减函数,在
上是减函数,在 上是增函数;②
上是增函数;② 是偶函数;
是偶函数; 处的切线与直线
处的切线与直线 垂直.
垂直.  的解析式;
的解析式; ,求函数
,求函数 在
在 上的最小值.
上的最小值.