Question

【题目】已知双曲线C1： =1，（a＞0，b＞0）的焦距是实轴长的2倍，若抛物线C2：x2=2py，（p＞0）的焦点到双曲线C1的渐近线的距离为2，求抛物线C2的标准方程．

Answer 1

【答案】解：∵双曲线C1： =1，（a＞0，b＞0）的焦距是实轴长的2倍，∴c=2a，即 =4，
∴ =3，
双曲线的一条渐近线方程为：bx﹣ay=0．
抛物线C2：x2=2py（p＞0）的焦点（0， ）到双曲线C1的渐近线的距离为2，
∴2= ，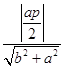
∵ =3，∴p=8．
∴抛物线C2的方程为x2=16y
【解析】利用双曲线C1： =1，（a＞0，b＞0）的焦距是实轴长的2倍，推出a，b的关系，求出抛物线的焦点坐标，通过点到直线的距离求出p，即可得到抛物线的方程．