题目内容
12.若非负实数x、y满足$\left\{\begin{array}{l}x+2y-4≥0\\ 2x+y-3≥0\end{array}\right.$,则x+y的最小值为$\frac{7}{3}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,求目标函数z=x+y的最小值.
解答 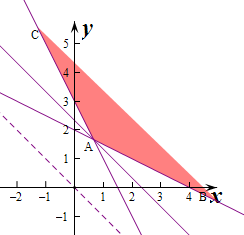 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
设z=x+y得y=-x+z,平移直线y=-x+z,
由图象可知当直线y=-x+z经过点A时,
直线y=-x+z的截距最小,此时z最小.
由$\left\{\begin{array}{l}{x+2y-4=0}\\{2x+y-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{5}{3}}\end{array}\right.$,即A($\frac{2}{3}$,$\frac{5}{3}$),
代入目标函数z=x+y得z=$\frac{2}{3}$+$\frac{5}{3}$=$\frac{7}{3}$.
即目标函数z=x+y的最小值为$\frac{7}{3}$.
故答案为:$\frac{7}{3}$.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
2.设全集“U=N,集合A={x∈N|log${\;}_{\frac{1}{2}}$x≤-1},则∁UA等于 ( )
| A. | {1,2} | B. | {1} | C. | {0,1,2} | D. | {0,1} |
7.”直线与抛物线相切”是“直线与抛物线只有一个公共点”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
17. 如图,在等腰直角△ABO中,OA=OB=1,C为AB上靠近点A的四等分点,过C作AB的垂线l,P为垂线上任一点,则$\overrightarrow{OP}•(\overrightarrow{OB}-\overrightarrow{OA)}$等于( )
如图,在等腰直角△ABO中,OA=OB=1,C为AB上靠近点A的四等分点,过C作AB的垂线l,P为垂线上任一点,则$\overrightarrow{OP}•(\overrightarrow{OB}-\overrightarrow{OA)}$等于( )
 如图,在等腰直角△ABO中,OA=OB=1,C为AB上靠近点A的四等分点,过C作AB的垂线l,P为垂线上任一点,则$\overrightarrow{OP}•(\overrightarrow{OB}-\overrightarrow{OA)}$等于( )
如图,在等腰直角△ABO中,OA=OB=1,C为AB上靠近点A的四等分点,过C作AB的垂线l,P为垂线上任一点,则$\overrightarrow{OP}•(\overrightarrow{OB}-\overrightarrow{OA)}$等于( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
1.已知不等式组$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$构成平面区域Ω(其中x,y是变量),若目标函数z=ax+6y(a>0)的最小值为-6,则实数a的值为( )
| A. | $\frac{3}{2}$ | B. | 6 | C. | 3 | D. | $\frac{1}{2}$ |