题目内容
17.某人午睡醒来,发现表停了,他打开收音机,想听电台整点报时,他等待的时间不多于15分钟的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 由电台整点报时的时刻是任意的知这是一个几何概型,电台整点报时知事件总数包含的时间长度是60,而他等待的时间不多于15分钟的事件包含的时间长度是15,利用时间的长度比即可求出所求
解答 解:由题意知这是一个几何概型,
∵电台整点报时,
∴事件总数包含的时间长度是60,
∵满足他等待的时间不多于15分钟的事件包含的时间长度是15,
由几何概型公式得到P=$\frac{15}{60}=\frac{1}{4}$;
故选C
点评 本题主要考查了几何概型,本题先要判断该概率模型,对于几何概型,它的结果要通过长度、面积或体积之比来得到,属于中档题

练习册系列答案
相关题目
9.经过如图程序,变量y的值为( )
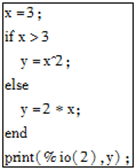
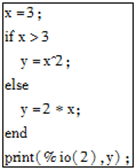
| A. | 3 | B. | 6 | C. | 9 | D. | 27 |
6.设函数f(x)在x处导数存在,则$\underset{lim}{△x→0}$$\frac{f(2)-f(2+△x)}{2△x}$=( )
| A. | -2f′(2) | B. | 2f′(2) | C. | -$\frac{1}{2}$f′(2) | D. | $\frac{1}{2}$f′(2) |
7.已知直线l1:2x+a2y+1=0,l2:ax-y-3=0,a=2是直线l1与直线l2垂直的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |