题目内容
【题目】在直角坐标系xOy,直线l的参数方程是 ![]() (t为参数).在以O为极点,x轴正半轴为极轴建立极坐标系中,曲线C:ρ=4sinθ.
(t为参数).在以O为极点,x轴正半轴为极轴建立极坐标系中,曲线C:ρ=4sinθ.
(1)当m=﹣1,α=30°时,判断直线l与曲线C的位置关系;
(2)当m=1时,若直线与曲l线C相交于A,B两点,设P(1,0),且||PA|﹣|PB||=1,求直线l的倾斜角.
【答案】
(1)解:由ρ=4sinθ,得ρ2=4ρsinθ,又ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得曲线C的普通方程为(x﹣2)2+y2=4,
所以曲线C是以M(2,0)为圆心,2为半径的圆,
由直线l的参数方程为 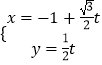 (t为参数),
(t为参数),
得直线l的直线坐标方程为 ![]() .
.
由圆心M到直线l的距离d= ![]() =
= ![]() <2,
<2,
故直线l与曲线C相交
(2)解:直线l为经过点P(1,0)倾斜角为α的直线,
由 ![]() ,代入(x﹣2)2+y2=4,整理得,t2﹣2tcosα﹣3=0,△=(2cosα)2+12>0,
,代入(x﹣2)2+y2=4,整理得,t2﹣2tcosα﹣3=0,△=(2cosα)2+12>0,
设A,B对应的参数分别为t1,t2,则t1+t2=2cosα,t1t2=﹣3<0,
所以t1,t2异号.则||PA|﹣|PB||=|t1+t2|=|2cosα|=1,
所以cosα=± ![]() ,又α∈[0,π),
,又α∈[0,π),
所以直线l的倾斜角α= ![]() 或
或 ![]()
【解析】(1)由题意利用ρ2=4ρsinθ,ρ2=x2+y2 , 将曲线C化为普通方程,将直线l的参数t消去为普通方程,圆心M到直线l的距离d与半径比较可得直线l与曲线C的位置关系.(2)设A,B对应的参数分别为t1 , t2 , 利用参数的几何意义建立关系,可得直线l的倾斜角.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案【题目】司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
开车时使用手机 | 开车时不使用手机 | 合计 | |
男性司机人数 | |||
女性司机人数 | |||
合计 |
(Ⅱ)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,若每次抽检的结果都相互独立,求X的分布列和数学期望E(X).
参考公式与数据: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
