题目内容
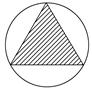
如图,在边长为5cm的正方形中挖去直角边长为4cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是__

9/25
解:因为均匀的粒子落在正方形内任何一点是等可能的
所以符合几何概型的条件.
设A=“粒子落在中间带形区域”则依题意得
正方形面积为:5×5=25
两个等腰直角三角形的面积为:2×1 /2 ×3×3=9
带形区域的面积为:25-9=16
∴P(A)=9/25,
则粒子落在中间带形区域的概率是9/25 .
所以符合几何概型的条件.
设A=“粒子落在中间带形区域”则依题意得
正方形面积为:5×5=25
两个等腰直角三角形的面积为:2×1 /2 ×3×3=9
带形区域的面积为:25-9=16
∴P(A)=9/25,
则粒子落在中间带形区域的概率是9/25 .

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
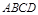 中,
中,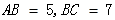 ,在其中任取一点
,在其中任取一点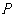 ,使满足
,使满足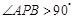 ,则
,则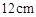 的线段
的线段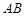 上任取一点
上任取一点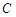 ,现作一矩形,使邻边长分别等于线段
,现作一矩形,使邻边长分别等于线段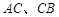 的长,则该矩形面积大于
的长,则该矩形面积大于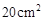 的概率为 .
的概率为 .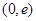 内随机取两个数,则这两个数之积不小于
内随机取两个数,则这两个数之积不小于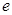 的概率为
的概率为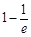

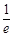
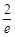
 围成的三角形区域有一个外接圆,在该圆内随机取一点,该点落在三角形内的概率是
围成的三角形区域有一个外接圆,在该圆内随机取一点,该点落在三角形内的概率是