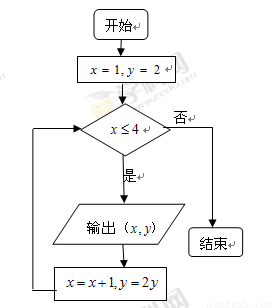
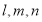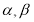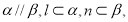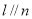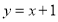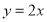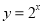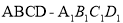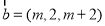题目内容
设 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比
的公比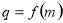 ,数列
,数列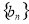 满足
满足
 ,
,
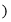 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和 .
.
(1)详见解析;(2) ;(3)
;(3)
【解析】
试题分析:(1)用公式
 将
将 化简可得
化简可得 间的关系,根据等比数列的定义可证得数列
间的关系,根据等比数列的定义可证得数列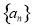 是等比数列。(2)属构造法求数列通项公式:因为
是等比数列。(2)属构造法求数列通项公式:因为
 ,所以
,所以 ,将其取倒数可推导出
,将其取倒数可推导出 ,根据等差数列的定义可知
,根据等差数列的定义可知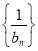 为等差数列,先求
为等差数列,先求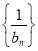 的通项公式,再求
的通项公式,再求 。(3)因为
。(3)因为 得通项公式为等差乘以等比数列所以应用错位相减法求数列的前
得通项公式为等差乘以等比数列所以应用错位相减法求数列的前 项和。将
项和。将 表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。
表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。
试题解析:(1)证明:当 时,
时, ,解得
,解得 . 1分
. 1分
当 时,
时,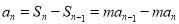 .即
.即 2分
2分
∵ 为常数,且
为常数,且 , ∴
, ∴
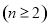 . 3分
. 3分
∴数列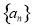 是首项为1,公比为
是首项为1,公比为 的等比数列. 4分
的等比数列. 4分
(2)【解析】
由(1)得,
 ,
,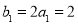 .
.
∵ , ∴
, ∴ ,即
,即
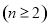 . 7分
. 7分
∴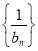 是首项为
是首项为 ,公差为1的等差数列. 8分
,公差为1的等差数列. 8分
∴ ,即
,即 (
(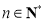 ). 9分
). 9分
(3)【解析】
由(2)知 ,则
,则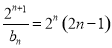 . 10分
. 10分
所以 ,
,
即
 , ①
, ①
则 ②
②
②-①得 ,
,
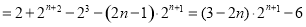
 . 14分
. 14分
考点:1等比数列的定义;2等差数列的定义及通项公式;3错位相减法求数列的和。

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目