题目内容
1.已知方程$\frac{x^2}{2-k}+\frac{y^2}{2k-1}$=1表示焦点在y轴上的椭圆,则实数k的取值范围是1<k<2.分析 利用方程$\frac{x^2}{2-k}+\frac{y^2}{2k-1}$=1表示焦点在y轴上的椭圆,可得2k-1>2-k>0,即可求出实数k的取值范围.
解答 解:∵方程$\frac{x^2}{2-k}+\frac{y^2}{2k-1}$=1表示焦点在y轴上的椭圆,
∴2k-1>2-k>0
∴1<k<2.
故答案为:1<k<2.
点评 本题考查实数k的取值范围,考查椭圆的标准方程,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.把函数y=ex的图象按向量$\overrightarrow{a}$=(2,0)平移,得到y=f(x)的图象,则f(x)=( )
| A. | ex+2 | B. | ex-2 | C. | ex+2 | D. | ex-2 |
16.已知$\overrightarrow a=({1,-1,1})$,则与向量$\overrightarrow a$共线的单位向量是( )
| A. | $\overrightarrow n=±({1,-1,1})$ | B. | $\overrightarrow n=±({\frac{1}{3},-\frac{1}{3},\frac{1}{3}})$ | C. | $\overrightarrow n=±({\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | D. | $\overrightarrow n=±({\frac{{\sqrt{3}}}{3},-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ |
6.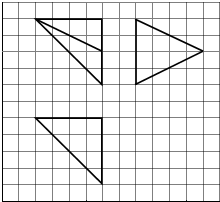 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )| A. | 8 | B. | $4\sqrt{5}$ | C. | 12 | D. | 16 |
13.已知a=log3650.99、b=1.01365、c=0.99365,则a、b、c的大小关系为( )
| A. | a<c<b | B. | b<a<c | C. | a<b<c | D. | b<c<a |
10.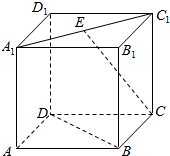 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 已知函数f(x)是R上的奇函数,且x>0时,f(x)=-x2+2x.
已知函数f(x)是R上的奇函数,且x>0时,f(x)=-x2+2x.