题目内容
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB=![]() AD,E是线段PD上的点,F是线段AB上的点,
AD,E是线段PD上的点,F是线段AB上的点,
且![]() .
.
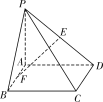
(1)证明:EF∥平面PBC;
(2)是否存在实数λ,使得异面直线EF与CD所成角为60°?若存在,试求出λ的值,若不存在,请说明理由.
【答案】(1)见证明;(2)见解析
【解析】
(1)作EH∥AD交PA于点H,连接HF,结合![]() ,可以证明FH∥PB,从而可以证明平面EFH∥平面PBC,进而得到EF∥平面PBC;(2)异面直线EF与CD所成角为60°,可知
,可以证明FH∥PB,从而可以证明平面EFH∥平面PBC,进而得到EF∥平面PBC;(2)异面直线EF与CD所成角为60°,可知![]() ,则
,则![]() ,再用λ分别表示出
,再用λ分别表示出![]() 与
与![]() ,代入即可求出λ.
,代入即可求出λ.
(1)作EH∥AD交PA于点H,连接HF,
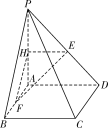
∵EH∥AD,∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴FH∥PB.
又∵EH∥AD,FH∩HE=H,
∴平面EFH∥平面PBC.
∵EF在平面EFH内,∴EF∥平面PBC.
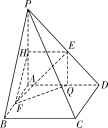
(2)存在实数![]() ,使得异面直线EF与CD所成角为60°.
,使得异面直线EF与CD所成角为60°.
其理由如下:假设存在实数λ,使得异面直线EF与CD所成角为60°,
∵AB∥CD,∴∠AFE为异面直线EF与CD所成角,
∴![]() .
.
过点E作EQ⊥AD交AD于点Q,连接FQ,
∵PA=AD,AB=![]() AD,∴设AD=1,
AD,∴设AD=1,
又∵![]() ,
,
可知![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∵![]() ,
,
∴![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() .
.
∴存在实数![]() ,使得异面直线EF与CD所成角为60°
,使得异面直线EF与CD所成角为60°

 阅读快车系列答案
阅读快车系列答案【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: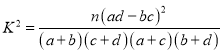 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|

