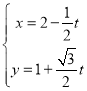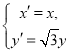题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1是边长为2的菱形,且CA=CB1.
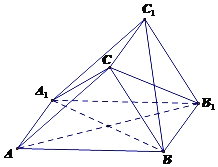
(1)证明:面CBA1⊥面CB1A;
(2)若∠BAA1=60°,A1C=BC=BA1,求点C到平面A1BC1的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)设A1B∩AB1=O,连接CO.证明A1B⊥AB1,CO⊥AB1,得到AB1⊥面CA1B,然后证明面CBA1⊥面CB1A.
(2)说明线段CH的长就是点C到平面A1BC1的距离.然后转化求解即可.
(1)证明:设A1B∩AB1=O,连接CO.因为侧面ABB1A1是菱形,所以A1B⊥AB1,
又因为CA=CB1,所以CO⊥AB1,又A1B∩CO=O,
所以AB1⊥面CA1B,又AB1面CAB1,所以面CBA1⊥面CB1A.
(2)在菱形ABB1A1中,因为∠BAA1=60°,
所以△ABA1是等边三角形,可得A1B=2,所以BC=2=BB1,
所以侧面BB1C1C是菱形,故CB1⊥C1B,(*)
在等边三角形CA1B中,A1B⊥CO,又A1B⊥AB1,且CO∩AB1=O,
所以A1B⊥面CAB1,又CB1面CAB1,所以CB1⊥A1B,
结合(*)以及A1B∩C1B=B得CB1⊥面A1C1B,设CB1∩C1B=H,
则线段CH的长就是点C到平面A1BC1的距离.
经计算得![]() ,
,![]() ,
,
所以![]() ,即点C到平面A1BC1的距离为
,即点C到平面A1BC1的距离为![]() .
.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目