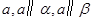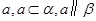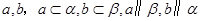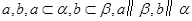题目内容
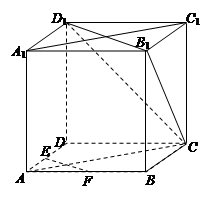
(本小题满分12分)如图,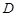 、
、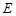 分别是正三棱柱
分别是正三棱柱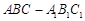 的棱
的棱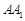 、
、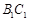 的中点,且棱
的中点,且棱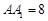 ,
,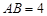 .
.
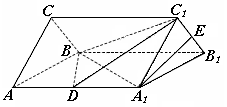
(Ⅰ)求证: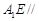 平面
平面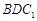 ;
;
(Ⅱ)在棱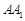 上是否存在一点
上是否存在一点 ,使二面角
,使二面角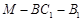 的大小为
的大小为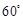 ,若存在,求
,若存在,求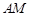 的长;若不存在,说明理由。
的长;若不存在,说明理由。
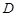 、
、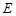 分别是正三棱柱
分别是正三棱柱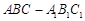 的棱
的棱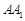 、
、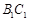 的中点,且棱
的中点,且棱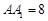 ,
,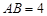 .
.
(Ⅰ)求证:
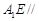 平面
平面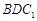 ;
;(Ⅱ)在棱
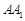 上是否存在一点
上是否存在一点 ,使二面角
,使二面角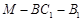 的大小为
的大小为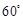 ,若存在,求
,若存在,求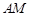 的长;若不存在,说明理由。
的长;若不存在,说明理由。(1)见解析;(2)故棱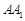 上不存在使二面角
上不存在使二面角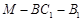 的大小为
的大小为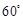 的点
的点 .
.
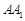 上不存在使二面角
上不存在使二面角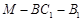 的大小为
的大小为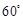 的点
的点 .
.本试题主要是考查线面平行的判定和二面角的求解综合运用。
(1)利用线面平行的判定定理,先证明线线平行,然后得到线面平行。
(2)在第二问中建立空间直角坐标系,利用平面的法向量,与法向量的夹角来表示二面角的平面角的求解。
【法一】(Ⅰ)在线段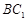 上取中点
上取中点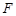 ,连结
,连结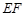 、
、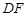 .
.
则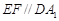 ,且
,且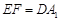 ,∴
,∴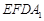 是平行四边形……2′
是平行四边形……2′
∴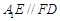 ,又
,又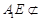 平面
平面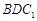 ,
,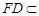 平面
平面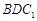 ,∴
,∴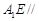 平面
平面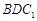 .……4
.……4

又∵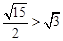 ,∴二面角
,∴二面角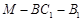 大于
大于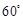 . ……11′
. ……11′
∴ 在棱
在棱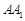 上时,二面角
上时,二面角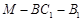 总大于
总大于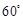 .
.
故棱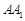 上不存在使二面角
上不存在使二面角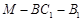 的大小为
的大小为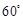 的点
的点 . ……12′
. ……12′
(1)利用线面平行的判定定理,先证明线线平行,然后得到线面平行。
(2)在第二问中建立空间直角坐标系,利用平面的法向量,与法向量的夹角来表示二面角的平面角的求解。
【法一】(Ⅰ)在线段
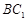 上取中点
上取中点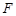 ,连结
,连结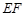 、
、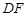 .
.则
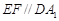 ,且
,且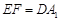 ,∴
,∴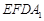 是平行四边形……2′
是平行四边形……2′∴
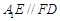 ,又
,又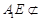 平面
平面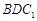 ,
,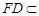 平面
平面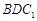 ,∴
,∴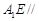 平面
平面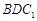 .……4
.……4
又∵
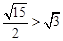 ,∴二面角
,∴二面角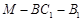 大于
大于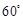 . ……11′
. ……11′∴
 在棱
在棱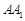 上时,二面角
上时,二面角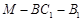 总大于
总大于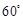 .
.故棱
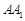 上不存在使二面角
上不存在使二面角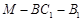 的大小为
的大小为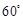 的点
的点 . ……12′
. ……12′
练习册系列答案
相关题目
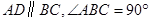 ,
,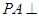 平面
平面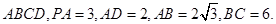
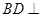 平面PAC;
平面PAC;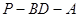 的大小.
的大小.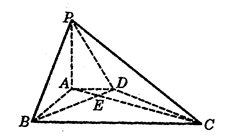
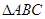 中,
中,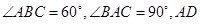 是
是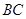 上的高,沿
上的高,沿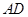 把
把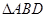 折起,使
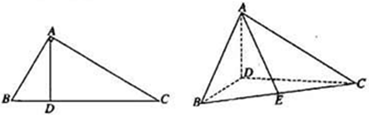
折起,使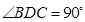 。
。
 中,
中,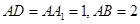 ,点
,点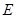 在棱
在棱 上移动
上移动 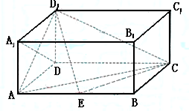
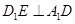 ;
; 的中点时,求点
的中点时,求点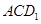 的距离;
的距离;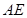 等于何值时,二面角
等于何值时,二面角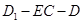 的大小为
的大小为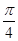
 是空间两条直线,
是空间两条直线,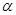 ,
,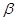 是空间两个平面,则下列选项中不正确的是( )
是空间两个平面,则下列选项中不正确的是( ) 时,“
时,“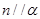 ”是“
”是“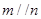 ”的必要不充分条件
”的必要不充分条件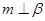 ”是“
”是“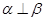 ”的充分不必要条件
”的充分不必要条件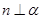 时, “
时, “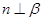 ”是“
”是“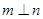 ”的充分不必要条件
”的充分不必要条件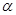 ,则b与
,则b与 平面
平面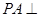 平面
平面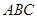 ,
,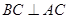 ,则图中直角三角形的个数为________.
,则图中直角三角形的个数为________.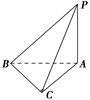
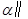 平面
平面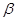 的是( )
的是( )