题目内容
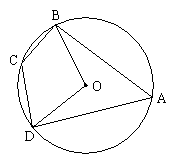
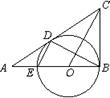
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.
⑴判断BE是否平分∠ABC,并说明理由;
⑵若AE=6,BE=8,求EF的长.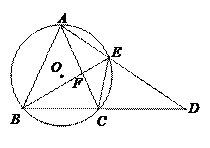
⑴判断BE是否平分∠ABC,并说明理由;
⑵若AE=6,BE=8,求EF的长.
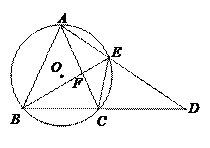
(1)即BE平分∠ABC;(2)EF= .
.
 .
. ⑴BE平分∠ABC.
∵CD=AC,∴∠D="∠CAD."
∵AB=AC,∴∠ABC=∠ACB
∵∠EBC=∠CAD,∴∠EBC="∠D=∠CAD. "
∵∠ABC=∠ABE+∠EBC,∠ACB=∠D+∠CAD,
∴∠ABE=∠EBC,即BE平分∠ABC.
⑵由⑴知∠CAD="∠EBC" =∠ABE.
∵∠AEF=∠AEB,∴△AEF∽△BEA.
∴ ,∵AE=6, BE=8.
,∵AE=6, BE=8.
∴EF= .
.
∵CD=AC,∴∠D="∠CAD."
∵AB=AC,∴∠ABC=∠ACB
∵∠EBC=∠CAD,∴∠EBC="∠D=∠CAD. "
∵∠ABC=∠ABE+∠EBC,∠ACB=∠D+∠CAD,
∴∠ABE=∠EBC,即BE平分∠ABC.
⑵由⑴知∠CAD="∠EBC" =∠ABE.
∵∠AEF=∠AEB,∴△AEF∽△BEA.
∴
 ,∵AE=6, BE=8.
,∵AE=6, BE=8.∴EF=
 .
. 
练习册系列答案
相关题目
 ,
,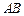 是圆
是圆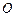 的的直径,点
的的直径,点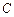 是弧
是弧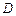 ,
,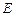 分别是
分别是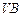 ,
,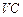 的中点,
的中点,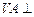
 .
.
 与
与 平面
平面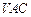 .
.
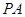 切
切 于点
于点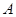 ,
,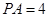 ,
,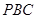 过圆心
过圆心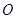 ,且与圆相交于
,且与圆相交于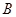 、
、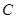 两点,
两点, ,则
,则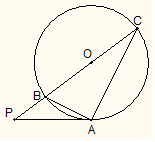
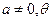 为参数,圆C:
为参数,圆C: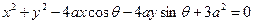
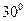 , PA=
, PA=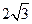 ,PC=1,则圆O的半径等于 .
,PC=1,则圆O的半径等于 .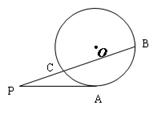
 通过不同的三点
通过不同的三点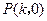 ,
,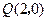 ,和
,和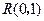 ,且该圆在点
,且该圆在点 处的切线的斜率等于1,求圆
处的切线的斜率等于1,求圆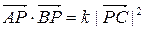 .
.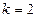 时,求
时,求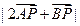 的最大、最小值.
的最大、最小值.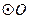 的内接四边形
的内接四边形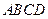 中,
中,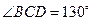 ,则
,则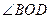 的度数是____________.
的度数是____________.