题目内容
已知A、B、C、D、E五点,A、B、C、D共面,B、C、D、E共面,则A、B、C、D、E五点一定共面吗?
在题设条件下,A、B、C、D、E五点不一定共面.
(1)当B、C、D三点不共线时,
由公理3可知B、C、D三点确定一个平面α,
由题设知A∈α,E∈α,故A、B、C、D、E五点共面.
(2)当B、C、D三点共线时,设共线于l,若A∈l,?E∈l?,
则A、B、C、D、E五点共面;
若A、E有且只有一点在l上,
则A、B、C、D、E五点共面;
若A、E都不在l上,则A、B、C、D、E可能不共面.
综上所述,在题设条件下,A、B、C、D、E五点不一定共面.
由公理3可知B、C、D三点确定一个平面α,
由题设知A∈α,E∈α,故A、B、C、D、E五点共面.
(2)当B、C、D三点共线时,设共线于l,若A∈l,?E∈l?,
则A、B、C、D、E五点共面;
若A、E有且只有一点在l上,
则A、B、C、D、E五点共面;
若A、E都不在l上,则A、B、C、D、E可能不共面.
综上所述,在题设条件下,A、B、C、D、E五点不一定共面.

练习册系列答案
相关题目
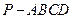 中,
中,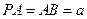 ,点
,点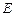 在棱
在棱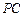 上。
上。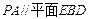 ,并加以证明;
,并加以证明;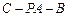 的余弦值。
的余弦值。
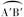 的长度是上底面圆周长的
的长度是上底面圆周长的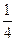 ,求由A爬到B的最短路程.
,求由A爬到B的最短路程. 中,底面是一个矩形,
中,底面是一个矩形, ,
, ,又
,又 ,
, ,
, .
. 的大小.(用反三角函数表示)
的大小.(用反三角函数表示)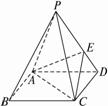
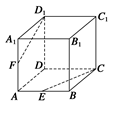
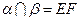 ,
,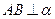 ,
,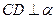 ,垂足分别为
,垂足分别为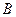 、
、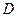 。若增加一个条件,就能推出
。若增加一个条件,就能推出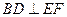 。现有:
。现有: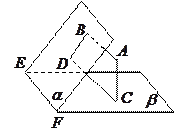
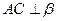 ;
;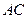 与
与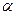 、
、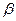 所成的角相等;
所成的角相等;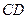 在
在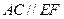 。
。