题目内容
A、B、C是表面积为64π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成角是
- A.30°
- B.45°
- C.60°
- D.不确定
C
分析:由题意截面ABC所在小圆,BC为直径,求出球的半径,即可求出直线OA与截面ABC所成角.
解答:由题意截面ABC所在小圆,BC为直径,A、B、C是表面积为64π的球的半径为:4πr2=64π,半径为4,即OA=4,BC 的中点与球心连线与截面ABC垂直,所以直线OA与截面ABC所成角的余弦为: ;直线OA与截面ABC所成角为:60°.
;直线OA与截面ABC所成角为:60°.
故选C
点评:本题是中档题,考查直线与平面所成角的求法,考查空间想象能力,计算能力,熟练掌握基本定理、基本方法是解决本题的关键.
分析:由题意截面ABC所在小圆,BC为直径,求出球的半径,即可求出直线OA与截面ABC所成角.
解答:由题意截面ABC所在小圆,BC为直径,A、B、C是表面积为64π的球的半径为:4πr2=64π,半径为4,即OA=4,BC 的中点与球心连线与截面ABC垂直,所以直线OA与截面ABC所成角的余弦为:
 ;直线OA与截面ABC所成角为:60°.
;直线OA与截面ABC所成角为:60°.故选C
点评:本题是中档题,考查直线与平面所成角的求法,考查空间想象能力,计算能力,熟练掌握基本定理、基本方法是解决本题的关键.

练习册系列答案
相关题目
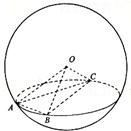 如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是( )
如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是( )A、arcsin
| ||||
B、arccos
| ||||
C、arcsin
| ||||
D、arccos
|
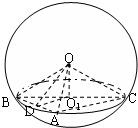 如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )
如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|
A、B、C是表面积为64π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成角是( )
| A、30° | B、45° | C、60° | D、不确定 |
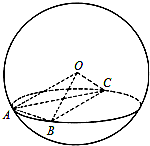 如图,A,B,C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是
如图,A,B,C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是