题目内容
给出下列四个命题:
①函数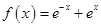 有最小值是
有最小值是 ;
;
②函数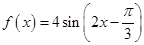 的图象关于点
的图象关于点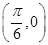 对称;
对称;
③若“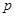 且
且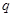 ”为假命题,则
”为假命题,则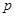 、
、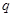 为假命题;
为假命题;
④已知定义在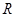 上的可导函数
上的可导函数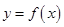 满足:对
满足:对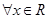 ,都有
,都有 成立,
成立,
若当 时,
时,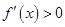 ,则当
,则当 时,
时,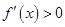 .
.
其中正确命题的序号是 .
①②④.
解析试题分析:对于命题①,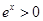 ,
,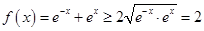 ,当且仅当
,当且仅当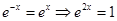 ,即当
,即当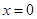 时,上式取等号,即函数
时,上式取等号,即函数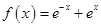 有最小值
有最小值 ,故命题①正确;对于命题②,由于
,故命题①正确;对于命题②,由于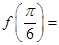
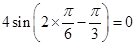 ,故函数
,故函数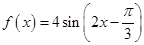 的图象关于点
的图象关于点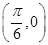 对称,故命题②正确;对于命题③,若“
对称,故命题②正确;对于命题③,若“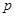 且
且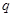 ”为假命题,则
”为假命题,则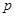 、
、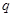 中至少有一个是假命题,故命题③错误;对于命题④,由于函数
中至少有一个是假命题,故命题③错误;对于命题④,由于函数 是奇函数,当
是奇函数,当 时,
时,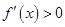 ,即函数
,即函数 在区间
在区间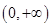 上单调递增,由奇函数的性质知,函数
上单调递增,由奇函数的性质知,函数 在
在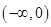 上也是单调递增的,即当
上也是单调递增的,即当 时,仍有
时,仍有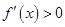 ,故命题④正确,综上所述,正确命题的序号是①②④.
,故命题④正确,综上所述,正确命题的序号是①②④.
考点:1.基本不等式;2.三角函数的对称性;3.复合命题;4.函数的奇偶性与单调性

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
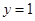 与曲线
与曲线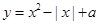 有四个交点,则实数
有四个交点,则实数 的取值范围是 .
的取值范围是 .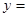
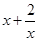 的值域为 .
的值域为 . 是奇函数,且当
是奇函数,且当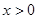 时,
时,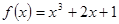 ,则当
,则当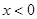 时,
时,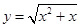 的定义域是____________.
的定义域是____________. 解集为空集,则满足条件的实数a的值为 .
解集为空集,则满足条件的实数a的值为 .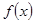 在
在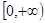 上是增函数,
上是增函数,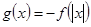 ,若
,若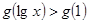 ,则x的取值范围是________________.
,则x的取值范围是________________. 与
与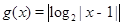 ,则关于
,则关于 与
与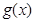 的下列说法正确的是 .
的下列说法正确的是 .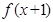 为偶函数;
为偶函数;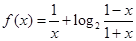 ,则
,则 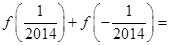 .
.