题目内容
已知函数f(x)=4 解集为空集,则满足条件的实数a的值为 .
解集为空集,则满足条件的实数a的值为 .
解析试题分析:因为函数f(x)=4x3-4ax,当x∈[0,1]时,关于x的不等式|f(x)|>1的解集为空集?当x∈[0,1]时,使得|f(x)|≤1恒成立,?x∈[0,1]时,-1≤4x3-4ax≤1恒成立,?x∈[0,1]时,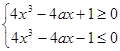 ?恒成立,当x=0时,由上式可以知道:无论a取何实数都使该式①恒成立;当x∈(0,1]时,由①可以等价于x∈(0,1]的一切数值均使得
?恒成立,当x=0时,由上式可以知道:无论a取何实数都使该式①恒成立;当x∈(0,1]时,由①可以等价于x∈(0,1]的一切数值均使得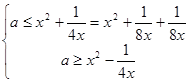 恒成立,即
恒成立,即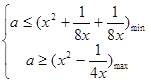 ,解得:
,解得: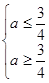 即:
即: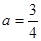 .
.
考点:1.考查函数在定义域内恒成立问题的等价转化;2.利用均值不等式及函数的单调性求函数的最值

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
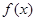 是
是 上的奇函数,
上的奇函数,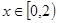 时,
时,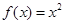 ,若对于任意
,若对于任意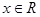 ,都有
,都有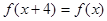 ,则
,则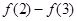 的值为 .
的值为 .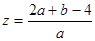 的取值范围是 .
的取值范围是 .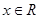 都有
都有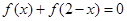 ,则f(x)是以2为周期的周期函数;
,则f(x)是以2为周期的周期函数;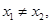 若
若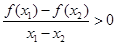 恒成立,则f(x)为
恒成立,则f(x)为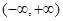 上的增函数.
上的增函数.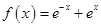 有最小值是
有最小值是 ;
;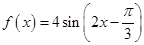 的图象关于点
的图象关于点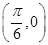 对称;
对称;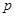 且
且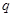 ”为假命题,则
”为假命题,则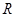 上的可导函数
上的可导函数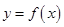 满足:对
满足:对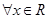 ,都有
,都有 成立,
成立, 时,
时,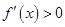 ,则当
,则当 时,
时,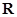 上的奇函数
上的奇函数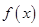 满足
满足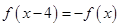 ,且
,且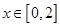 时,
时,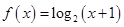 ,有下列结四个论:
,有下列结四个论: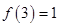 ;
;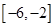 上是增函数;
上是增函数;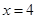 对称;
对称;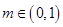 ,则关于
,则关于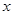 的方程
的方程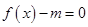 在
在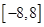 上所有根之和为-8.
上所有根之和为-8.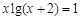 有 个不同的实数根
有 个不同的实数根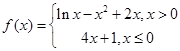 的零点个数是 .
的零点个数是 .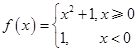 ,则满足不等式
,则满足不等式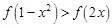 的
的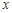 的取值范围是 .
的取值范围是 .