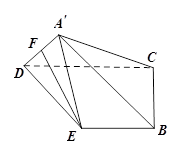
题目内容
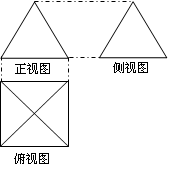
一个多面体的直观图和三视图如下:(其中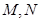 分别是
分别是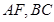 中点)
中点)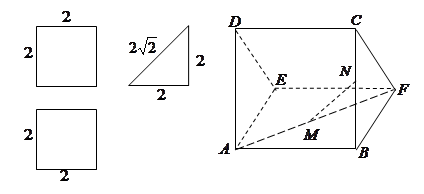
(1)求证: 平面
平面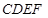 ;
;
(2)求多面体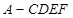 的体积.
的体积.
(1)见解析;(2) 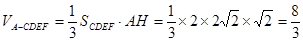 。
。
解析试题分析:(1)由三视图知,该多面体是底面为直角三角形的直三棱柱,那么结合棱柱的性质可知结论成立。
(2)由三视图可知,该多面体是底面为等腰直角三角形的直三棱柱,在直三棱柱中,两个侧面是边长为2的正方形,得到四棱锥的高AE=2,根据四棱锥的体积公式得到结果.
解:
(1)由三视图知,该多面体是底面为直角三角形的直三棱柱,且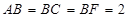 ,
,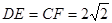 ,∴
,∴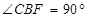 . ---2分
. ---2分
取 中点
中点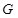 ,连
,连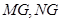 ,由
,由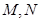 分别是
分别是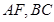 中点,可设:
中点,可设: ,
,
∴面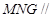 面
面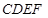 ∴
∴ 面
面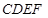 … ---8分
… ---8分
(2)作 于
于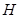 ,由于三棱柱
,由于三棱柱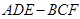 为直三棱柱
为直三棱柱
∴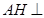 面
面 ,
,
且 ∴
∴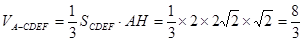 ,---12
,---12
考点:本题主要考查了线面平行的判定定理的运用,以及几何体体积的运算。
点评:解决该试题的关键是能利用三视图还原为几何体,结合几何体的结构特点和公式得到其体积,以及线面的平行的判定。

练习册系列答案
相关题目
 的正三角形,O是底面圆心.
的正三角形,O是底面圆心.
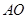 的中点
的中点 作平行于圆锥底面的截面,求截得的圆台的体积.
作平行于圆锥底面的截面,求截得的圆台的体积.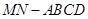 , 下半部分是长方体
, 下半部分是长方体 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.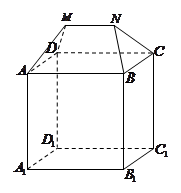

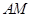 与平面
与平面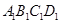 所成角的正弦值;
所成角的正弦值;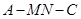 的余弦值;
的余弦值; 中,底面
中,底面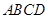 是直角梯形,
是直角梯形,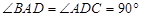 ,
, ,
,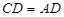 .
.
 是二面角
是二面角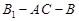 的平面角;
的平面角; 上是否存一点
上是否存一点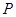 ,使得
,使得 与平面
与平面 与平面
与平面 都平行?证明你的结论.
都平行?证明你的结论.
 ),则该几何体的体积。
),则该几何体的体积。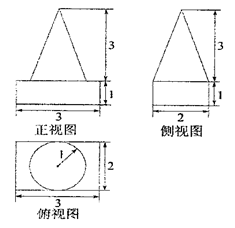
 经过平面
经过平面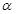 内一定点
内一定点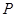 ,但
,但 ,使平面
,使平面 的中点. ks5u
的中点. ks5u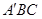 ;
; 与平面
与平面