题目内容
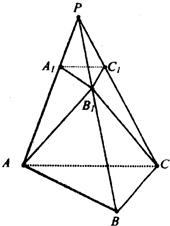 (2008•河西区三模)如图,已知三棱锥P-ABC,A1,B1,C1分别在棱PA、PB、PC上,且面A1B1C1∥面ABC,又面AB1C⊥面ABC.△AB1C为边长是4的等边三角形,∠ACB=90°,BC=2.
(2008•河西区三模)如图,已知三棱锥P-ABC,A1,B1,C1分别在棱PA、PB、PC上,且面A1B1C1∥面ABC,又面AB1C⊥面ABC.△AB1C为边长是4的等边三角形,∠ACB=90°,BC=2.(1)求证:B1C1⊥AB1;
(2)求点A到平面PBC的距离;
(3)求二面角A-PB-C的大小.
分析:(1)由面面垂直的性质定理可得BC⊥面ABC1,进而BC⊥AB1,由面面平行的性质定理可得B1C1∥BC,最后可得B1C1⊥AB1;
(2)过A作AD⊥B1C于D,可证得AD⊥面PBC,即AD长即为点A到面PBC的距离,解三角形AB1C,可得答案.
(3)过D点DM⊥PB于M,连AM,由三垂线定理知AM⊥PB,即∠AMD是二面角A-PB-C的平面角,解Rt△AMD可得答案.
(2)过A作AD⊥B1C于D,可证得AD⊥面PBC,即AD长即为点A到面PBC的距离,解三角形AB1C,可得答案.
(3)过D点DM⊥PB于M,连AM,由三垂线定理知AM⊥PB,即∠AMD是二面角A-PB-C的平面角,解Rt△AMD可得答案.
解答:证明: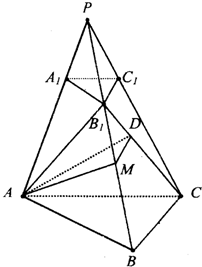 (1)∵面AB1C⊥面ABC,面AB1C∩面ABC=AC,BC⊥AC
(1)∵面AB1C⊥面ABC,面AB1C∩面ABC=AC,BC⊥AC
∴BC⊥面ABC1(2分)
∴BC⊥AB1
又∵面A1B1C1∥面ABC
面PBC∩面A1B1C1=B1C1,面PBC∩面ABC=BC
∴B1C1∥BC
∴B1C1⊥AB1(4分)
解:(2)过A作AD⊥B1C于D
∴△AB1C为等边三角形
∴D为B1C的中点
又∵BC⊥平面AB1C,AD?平面AB1C,
∴BC⊥AD
又∵B1C∩BC=C,B1C,BC?面B1BC
∴AD⊥面B1BC
即AD⊥面PBC
∴AD长即为点A到面PBC的距离(6分)
在正三角形AB1C中,AC=4
∴AD=
AC=2
(8分)
(3)过D点DM⊥PB于M,连AM,由三垂线定理知AM⊥PB
∴∠AMD是二面角A-PB-C的平面角(10分)
在Rt△AMD中,AD=2
△B1DM∽△B1BC
∴
=
又B1B=
=2
∴DM=
=
=
∴tan∠AMD=
=
∴二面角A-PB-C的大小为arctan
(12分)
 (1)∵面AB1C⊥面ABC,面AB1C∩面ABC=AC,BC⊥AC
(1)∵面AB1C⊥面ABC,面AB1C∩面ABC=AC,BC⊥AC∴BC⊥面ABC1(2分)
∴BC⊥AB1
又∵面A1B1C1∥面ABC
面PBC∩面A1B1C1=B1C1,面PBC∩面ABC=BC
∴B1C1∥BC
∴B1C1⊥AB1(4分)
解:(2)过A作AD⊥B1C于D
∴△AB1C为等边三角形
∴D为B1C的中点
又∵BC⊥平面AB1C,AD?平面AB1C,
∴BC⊥AD
又∵B1C∩BC=C,B1C,BC?面B1BC
∴AD⊥面B1BC
即AD⊥面PBC
∴AD长即为点A到面PBC的距离(6分)
在正三角形AB1C中,AC=4
∴AD=
| ||
| 2 |
| 3 |
(3)过D点DM⊥PB于M,连AM,由三垂线定理知AM⊥PB
∴∠AMD是二面角A-PB-C的平面角(10分)
在Rt△AMD中,AD=2
| 3 |
△B1DM∽△B1BC
∴
| DM |
| BC |
| B1D |
| B1B |
| BC2+B1C2 |
| 5 |
∴DM=
| BC•B1D |
| B1B |
| 2×2 | ||
2
|
| 2 | ||
|
∴tan∠AMD=
| AD |
| DM |
| 15 |
∴二面角A-PB-C的大小为arctan
| 15 |
点评:本题考查的知识点是二面角的平面角及求法,点到平面的距离,线线垂直,线面垂直及面面垂直之间的转化,是空间立体几何的综合应用,难度中档.

练习册系列答案
相关题目