题目内容
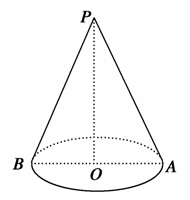
圆锥底面半径为1,高为2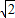 ,轴截面为PAB,如图,从A点拉一绳子绕圆锥侧面一周回到A点,求最短绳长和圆锥的侧面积.
,轴截面为PAB,如图,从A点拉一绳子绕圆锥侧面一周回到A点,求最短绳长和圆锥的侧面积.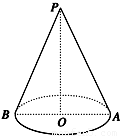
【答案】分析:将圆锥表面展开,最短绳长为展开图中两点直线距离,再求出母线,得到侧面积.
解答:解:将圆锥表面展开,得到如图所示的扇形.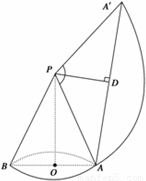
OA=1,PO=2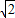 ,∴PA=3,∴
,∴PA=3,∴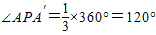
作PD⊥AA′,则∠APD=60°,∴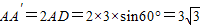
 最短绳长为3
最短绳长为3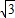 ,
,
母线长l=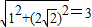 ,
,
圆锥的侧面积=πrl=3π
点评:本题考查圆锥的结构特征,转化能力与计算,将空间问题转化为平面问题是空间几何体中基本的方法.
解答:解:将圆锥表面展开,得到如图所示的扇形.

OA=1,PO=2
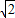 ,∴PA=3,∴
,∴PA=3,∴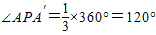
作PD⊥AA′,则∠APD=60°,∴
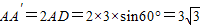
 最短绳长为3
最短绳长为3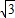 ,
,母线长l=
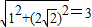 ,
,圆锥的侧面积=πrl=3π
点评:本题考查圆锥的结构特征,转化能力与计算,将空间问题转化为平面问题是空间几何体中基本的方法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 圆锥底面半径为1,高为2
圆锥底面半径为1,高为2