题目内容
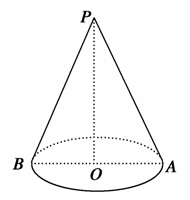
圆锥底面半径为1,高为2![]() ,轴截面为PAB,如图,从A点拉一绳子绕圆锥侧面一周回到A点,求最短绳长.
,轴截面为PAB,如图,从A点拉一绳子绕圆锥侧面一周回到A点,求最短绳长.
[解析] ∵OA=1,PO=2![]() ,
,
∴PA=3,
∴∠APA′=![]() ×360°=120°,
×360°=120°,

作PD⊥AA′,则∠APD=60°
∴AA′=2AD=2×3×sin60°=3![]() ,
,
∴最短绳长为3![]() .
.
[点评] 一般地,多面体或旋转体绕侧面或表面最短距离的问题,除球外,基本都是通过展开图来解决,关键是找准剪开的线,准确用展开图中的某条线段来表示这个最短距离,另外这里的所谓最短距离,实质是沿多面体或旋转体侧(表)面的最短路径,请思考下题:

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 圆锥底面半径为1,高为2
圆锥底面半径为1,高为2