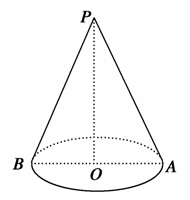
题目内容
圆锥底面半径为1,高为
,其中有一个内接正方体,求这个内接正方体的棱长是( )
| 2 |
分析:作出圆锥经过正方体上底面对角线的截面,得圆锥的轴截面SEF和正方体对角面CDD1C1,如图所示.作SO⊥EF于O,可得S0=
且OE=1,设正方体棱长为x,利用三角形相似建立关系式解出x的值,即可得到该正方体的棱长.
| 2 |
解答:解:过圆锥的顶点S和正方体底面的一条对角线CD作圆锥的截面,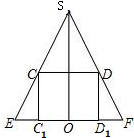 如图所示
如图所示
可得圆锥的轴截面SEF和正方体对角面CDD1C1,
设正方体棱长为x,则CC1=x,C1D1=
x
作SO⊥EF于O,可得S0=
且OE=1,
∵△ECC1∽△EOS,
∴
=
,代入数据得
=
解之得x=
,即内接正方体棱长为
故选:C
 如图所示
如图所示可得圆锥的轴截面SEF和正方体对角面CDD1C1,
设正方体棱长为x,则CC1=x,C1D1=
| 2 |
作SO⊥EF于O,可得S0=
| 2 |
∵△ECC1∽△EOS,
∴
| CC1 |
| SO |
| EC1 |
| EO |
| x | ||
|
1-
| ||||
| 1 |
解之得x=
| ||
| 2 |
| ||
| 2 |
故选:C
点评:本题给出圆锥的内接正方体,在已知圆锥的底面半径和高的情况下求内接正方体的棱长,着重考查了圆锥的性质、正方体的性质、组合图形的结构特征和相似三角形等知识,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 圆锥底面半径为1,高为2
圆锥底面半径为1,高为2