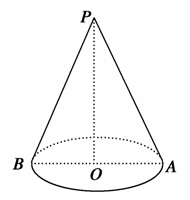
题目内容
 圆锥底面半径为1,高为2
圆锥底面半径为1,高为2| 2 |
分析:将圆锥表面展开,最短绳长为展开图中两点直线距离,再求出母线,得到侧面积.
解答:解:将圆锥表面展开,得到如图所示的扇形.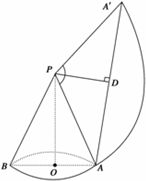
OA=1,PO=2
,∴PA=3,∴∠APA′=
×360°=120°
作PD⊥AA′,则∠APD=60°,∴AA′=2AD=2×3×sin60°=3
最短绳长为3
,
母线长l=
=3,
圆锥的侧面积=πrl=3π

OA=1,PO=2
| 2 |
| 1 |
| 3 |
作PD⊥AA′,则∠APD=60°,∴AA′=2AD=2×3×sin60°=3
| 3 |
|
| 3 |
母线长l=
12+(2
|
圆锥的侧面积=πrl=3π
点评:本题考查圆锥的结构特征,转化能力与计算,将空间问题转化为平面问题是空间几何体中基本的方法.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目