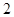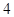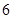题目内容
(本题满分14分)等差数列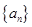 的首项为
的首项为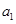 ,公差
,公差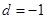 ,前
,前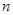 项和为
项和为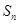
(Ⅰ)若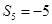 ,求
,求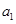 的值;
的值;
(Ⅱ)若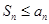 对任意正整数
对任意正整数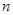 均成立,求
均成立,求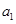 的取值范围。
的取值范围。
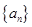 的首项为
的首项为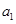 ,公差
,公差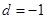 ,前
,前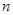 项和为
项和为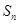
(Ⅰ)若
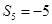 ,求
,求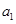 的值;
的值;(Ⅱ)若
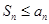 对任意正整数
对任意正整数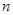 均成立,求
均成立,求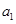 的取值范围。
的取值范围。(Ⅰ)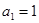 ;(Ⅱ)
;(Ⅱ) 。
。
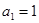 ;(Ⅱ)
;(Ⅱ) 。
。本试题主要是考查了等差数列的前n项和与其通项公式之间的关系的转化。
(1)利用数列的前n项和公式可知得到首项与公差的关系式,那么可知结论。
(2)利用不等式关系,结合通项公式可知化简为关于n的不等式,然后讨论得到。
(Ⅰ)由条件得,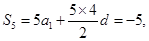 ………………………3分
………………………3分
解得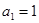 ………………………5分
………………………5分
(Ⅱ)由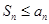 ,代人得
,代人得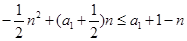 ………………………7分
………………………7分
整理,变量分离得: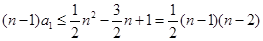 ………………9分
………………9分
当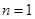 时,上式成立 …………………………10分
时,上式成立 …………………………10分
当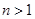 时,
时,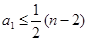 …………………………11分
…………………………11分
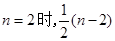 取到最小值
取到最小值 , ………12分
, ………12分
 ………………………… 14分
………………………… 14分
(1)利用数列的前n项和公式可知得到首项与公差的关系式,那么可知结论。
(2)利用不等式关系,结合通项公式可知化简为关于n的不等式,然后讨论得到。
(Ⅰ)由条件得,
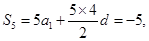 ………………………3分
………………………3分解得
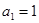 ………………………5分
………………………5分(Ⅱ)由
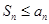 ,代人得
,代人得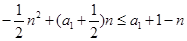 ………………………7分
………………………7分整理,变量分离得:
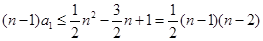 ………………9分
………………9分当
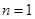 时,上式成立 …………………………10分
时,上式成立 …………………………10分当
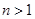 时,
时,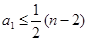 …………………………11分
…………………………11分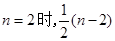 取到最小值
取到最小值 , ………12分
, ………12分  ………………………… 14分
………………………… 14分
练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 的前三项为
的前三项为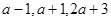 ,则此数列的通项公式为______ .
,则此数列的通项公式为______ .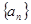 满足
满足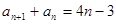
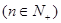 .
.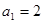 ,
,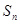 为
为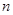 项和,求
项和,求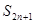 .
. 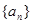 ,
,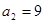 ,
,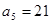 ,
,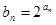 ,求数列
,求数列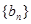 的前
的前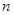 项和
项和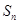 。
。 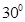 B、
B、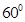 C、
C、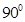 D、
D、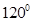
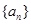 为等差数列,且
为等差数列,且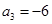 ,
,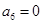 .
.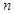 项和
项和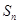 的最小值;
的最小值;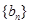 满足
满足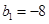 ,
,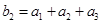 ,求
,求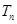 .
. 满足
满足 则
则 ( )
( )