Question

（本题满分14分）

已知关于的一元二次函数

（Ⅰ）设集合P={1，2， 3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作

为和，求函数在区间[上是增函数的概率；

（Ⅱ）设点（，）是区域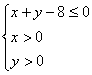内的随机点，求函数上是增函数的概率.

Answer 1

解：（Ⅰ）∵函数的图象的对称轴为

要使在区间上为增函数，

当且仅当>0且       ……………………………3分

若=1则=－1，

若=2则=－1，1

若=3则=－1，1；                 ……………………………5分

∴事件包含基本事件的个数是1+2+2=5

∴所求事件的概率为             ……………………………7分

（Ⅱ）由（Ⅰ）知当且仅当且>0时，

函数上为增函数，

依条件可知试验的全部结果所构成的区域为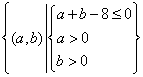

构成所求事件的区域为三角形部分。  ………………………………9分

由 ……………………………11分

∴所求事件的概率为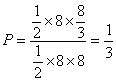 ……………………………　14分