题目内容

设a、b、m都是正整数，且a＜b，则下列不等式中恒成立的是（　　）
A、
a
b
＜
a+m
b+m
＜1
B、
a
b
≥
a+m
b+m
C、
a
b
≤
a+m
b+m
≤1
D、1＜
a+m
b+m
＜
a
b
分析：本题为分式比较大小问题，注意到a、b、m都是正整数，可用分析法转化为整式比较大小，利用基本不等式的性质即可；
也可利用做差比较法处理．
解答：解：a＜b且a、b、m都是正整数，
由不等式的性质可得am＜bm
∴am+ab＜bm+ab
即a（b+m）＜b（a+m）
∴
a
b
＜
a+m
b+m

又因为a＜b可得a+m＜b+m
∴
a+m
b+m
＜1
故选A
点评：本题考查不等式的性质、证明不等式等知识，属基本知识、基本题型的考查．
练习册系列答案
相关题目
设A（x1，y1），B（x2，y2）是函数f（x）=
1
2
+log2
x
1-x
图象上任意两点，且
OM
=
1
2
(
OA
+
OB
)，已知点M的横坐标为
1
2
．
（1）求点M的纵坐标；
（2）若Sn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*且n≥2，
①求Sn；
②已知an=
2
3
，n=1
1
(Sn+1)(Sn+1+1)
，n≥2
，其中n∈N*，Tn为数列{an}的前n项和，若Tn≤λ（Sn+1+1）对一切n∈N*都成立，试求λ的最小正整数值．
设A（x1，y1），B（x2，y2）是函数f（x）=
1
2
+log2
x
1-x
图象上任意两点，且
OM
=
1
2
（
OA
+
OB
），已知点M的横坐标为
1
2
，且有Sn=f（
1
n
）+f（
2
n
）+…+f（
n-1
n
），其中n∈N*且n≥2，
（1）求点M的纵坐标值；
（2）求s2，s3，s4及Sn；
（3）已知an=
1
(Sn+1)(Sn+1+1)
，其中n∈N*，且Tn为数列{an}的前n项和，若Tn≤λ（Sn+1+1）对一切n∈N*都成立，试求λ的最小正整数值．
设A（x1，y1），B（x2，y2）是函数f（x）=
1
2
+log2
x
1-x
图象上任意两点，且
OM
=
1
2
(
OA
+
OB
)，已知点M的横坐标为
1
2
．
（1）求点M的纵坐标；
（2）若Sn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*且n≥2，
①求Sn；
②已知
1
12
，其中n∈N*，Tn为数列{an}的前n项和，若Tn≤λ（Sn+1+1）对一切n∈N*都成立，试求λ的最小正整数值．
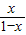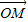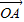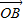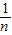设A（x1，y1），B（x2，y2）是函数f（x）=+log2图象上任意两点，且=（+），已知点M的横坐标为，且有Sn=f（）+f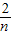（）+…+f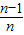（），其中n∈N*且n≥2，
（1）求点M的纵坐标值；
（2）求s2，s3，s4及Sn；
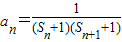（3）已知，其中n∈N*，且Tn为数列{an}的前n项和，若Tn≤λ（Sn+1+1）对一切n∈N*都成立，试求λ的最小正整数值．
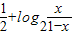设A（x1，y1），B（x2，y2）是函数f（x）=图象上任意两点，且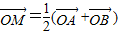，已知点M的横坐标为．
（1）求点M的纵坐标；
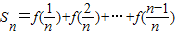（2）若，其中n∈N*且n≥2，
①求Sn；
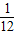②已知，其中n∈N*，Tn为数列{an}的前n项和，若Tn≤λ（Sn+1+1）对一切n∈N*都成立，试求λ的最小正整数值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网