题目内容
设A(x1,y1),B(x2,y2)是函数f(x)=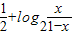 图象上任意两点,且
图象上任意两点,且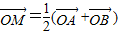 ,已知点M的横坐标为
,已知点M的横坐标为 .
.(1)求点M的纵坐标;
(2)若
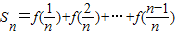 ,其中n∈N*且n≥2,
,其中n∈N*且n≥2,①求Sn;
②已知
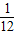 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.
【答案】分析:(1)由题设条件知M是AB的中点,由中点坐标公式可以求出M点的给坐标.
(2)①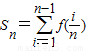 =
= ,即
,即 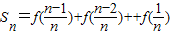 以上两式相加后两边再同时除以2就得到Sn.②当n≥2时,根据题设条件,由Tn<λ(Sn+1+1)得
以上两式相加后两边再同时除以2就得到Sn.②当n≥2时,根据题设条件,由Tn<λ(Sn+1+1)得 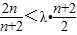 ,∴
,∴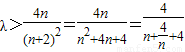 ,再由均值不等式求出λ的取值范围.
,再由均值不等式求出λ的取值范围.
解答:解:(1)依题意由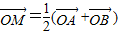 知M为线段AB的中点.
知M为线段AB的中点.
又∵M的横坐标为1,A(x1,y1),B(x2,y2)即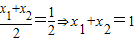
∴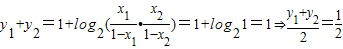
即M点的纵坐标为定值 .
.
(2)①由(Ⅰ)可知f(x)+f(1-x)=1,
又∵n≥2时
∴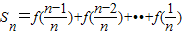
两式想加得,2Sn=n-1
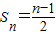
②当n≥2时,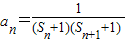 =
=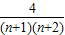 =4(
=4(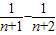 )
)
又n=1时,a1= 也适合.
也适合.
∴an=4(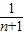 -
- )
)
∴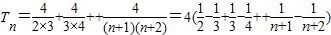 =
=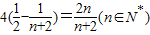
由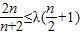 恒成立
恒成立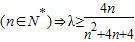
而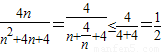 (当且仅当n=2取等号)
(当且仅当n=2取等号)
∴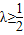 ,∴λ的最小正整数为1.
,∴λ的最小正整数为1.
点评:本题考查了数列与函数、函数的图象、不等式等综合内容,函数图象成中心对称的有关知识,考查相关方法,考查了数列中常用的思想方法,如倒序相加法,裂项相消法求数列前n项的和,利用函数与方程的思想,转化与化归思想解答热点问题--有关恒成立问题.
(2)①
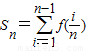 =
= ,即
,即 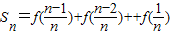 以上两式相加后两边再同时除以2就得到Sn.②当n≥2时,根据题设条件,由Tn<λ(Sn+1+1)得
以上两式相加后两边再同时除以2就得到Sn.②当n≥2时,根据题设条件,由Tn<λ(Sn+1+1)得 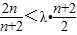 ,∴
,∴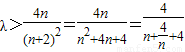 ,再由均值不等式求出λ的取值范围.
,再由均值不等式求出λ的取值范围.解答:解:(1)依题意由
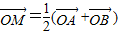 知M为线段AB的中点.
知M为线段AB的中点.又∵M的横坐标为1,A(x1,y1),B(x2,y2)即
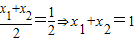
∴
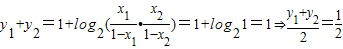
即M点的纵坐标为定值
 .
.(2)①由(Ⅰ)可知f(x)+f(1-x)=1,
又∵n≥2时

∴
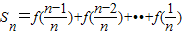
两式想加得,2Sn=n-1
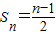
②当n≥2时,
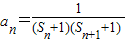 =
=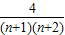 =4(
=4(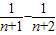 )
)又n=1时,a1=
 也适合.
也适合.∴an=4(
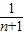 -
- )
) ∴
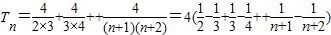 =
=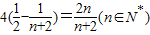
由
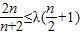 恒成立
恒成立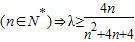
而
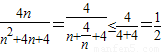 (当且仅当n=2取等号)
(当且仅当n=2取等号)∴
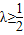 ,∴λ的最小正整数为1.
,∴λ的最小正整数为1.点评:本题考查了数列与函数、函数的图象、不等式等综合内容,函数图象成中心对称的有关知识,考查相关方法,考查了数列中常用的思想方法,如倒序相加法,裂项相消法求数列前n项的和,利用函数与方程的思想,转化与化归思想解答热点问题--有关恒成立问题.

练习册系列答案
相关题目
