题目内容
在边长为1的正三角形ABC中，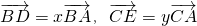
，x＞0，y＞0，且x+y=1，则
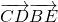的最大值为
- A.
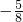
- B.
- C.
- D.
B
分析：根据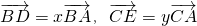，可得
=
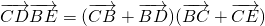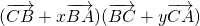=-1+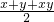
，利用x＞0，y＞0，且x+y=1，可求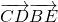的最大值．
解答：由题意，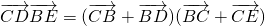
∵
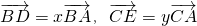
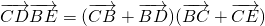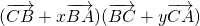∴==-1+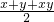
∵x＞0，y＞0，且x+y=1
∴xy≤
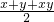∴-1+=-1+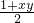
≤
当且仅当x=y=
时，取等号
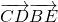∴当x=y=时，的最大值为
故选B
点评：本题考查向量知识的运用，考查向量的加法，考查向量的数量积，考查基本不等式的运用，综合性强．
分析：根据
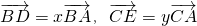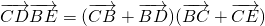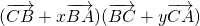，可得==-1+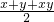，利用x＞0，y＞0，且x+y=1，可求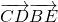的最大值．解答：由题意，
∵
∴
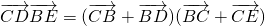
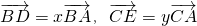
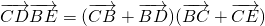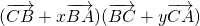==-1+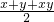∵x＞0，y＞0，且x+y=1
∴xy≤
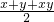∴-1+
=-1+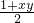≤当且仅当x=y=
时，取等号∴当x=y=
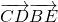时，的最大值为故选B
点评：本题考查向量知识的运用，考查向量的加法，考查向量的数量积，考查基本不等式的运用，综合性强．
练习册系列答案
相关题目