题目内容

在边长为1的正三角形ABC中，
BD
=
1
3
BA
，E是CA的中点，则
CD
•
BE
=（　　）
分析：结合已知，可先用
AB
，
AC
为一组基地表示向量
CD
，
BE
，结合向量的数量积的运算性质及数量积的定义可求
解答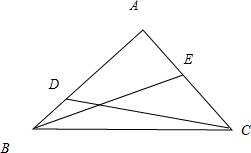：解：由题意可得，
CD
=
CB
+
BD
=
CB
+
1
3
BA
=
AB
-
AC
+
1
3
BA
=
2
3
AB
-
AC

BE
=
BC
+
CE
=
AC
-
AB
+
1
2
CA
=
1
2
AC
-
AB

∵
AB
•
AC
=1×1×cos60°=
1
2

∴
CD
•
BE
=（
2
3
AB
-
AC
）•（
1
2
AC
-
AB
）=
1
3
AB
•
AC
-
2
3
AB
2-
1
2
AC
2+
AB
•
AC

=
4
3
×
1
2
-
2
3
×1-
1
2
×1=-
1
2

故选B
点评：本题主要考查了向量的数量积的定义的简单应用，解题的关键是用
AB
，
AC
为一组基地表示向量
CD
，
BE
，
练习册系列答案
相关题目
在边长为1的正三角形ABC中，设
BC
=
a
，
AB
=
c
，
AC
=
b
，则
a
•
b
+
b
•
c
+
c
•
a
的值是
 
在边长为1的正三角形ABC中，
BC
=
a
，
AB
=
c
，
CA
=
b
，则
a
•
b
+
b
•
c
+
c
•
a
=（　　）
在边长为1的正三角形ABC中，
BD
=x
BA
，
CE
=y
CA
，x＞0，y＞0，且x+y=1，则
CD
•
BE
的最大值为（　　）
（2013•广元二模）在边长为1的正三角形ABC中，
AB
•
BC
+
BC
•
CA
+
CA
•
AB
=
-
3
2
-
3
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网