题目内容
7.已知圆x2+y2=4,圆内定点P(1,0),过P作两条互相垂直的弦AC和BD,设AC的倾斜角为可α(0$≤α<\frac{π}{2}$).(1)求四边形ABCD的面积S;
(2)当S取最大值时,求α及最大面积.
分析 (1)分别求出两条弦所在直线的点斜式方程,利用圆的弦长公式,求出AC和BD,再由S=$\frac{1}{2}$AC•BD得到答案;
(2)根据(1)中函数解析式,令t=$\frac{1}{{k}^{2}+1}$,结合二次函数的图象和性质,可得S取最大值时,α及最大面积的值.
解答 解:(1)∵AC的倾斜角为可α(0$≤α<\frac{π}{2}$).
当a=0时,AC即为x2+y2=4的直径,
此时AC=4,BD=2$\sqrt{{2}^{2}-{1}^{2}}$=2$\sqrt{3}$,
四边形ABCD的面积S=$\frac{1}{2}$AC•BD=4$\sqrt{3}$;
当a≠0时,设AC的斜率为k,则BD的斜率为$-\frac{1}{k}$,
则直线AC和BD的方程分别为:y=k(x-1)和y=$-\frac{1}{k}$(x-1),
即kx-y-k=0和x+ky-1=0,
此时圆心到AC和BD的距离分别为:$\frac{k}{\sqrt{1+{k}^{2}}}$和$\frac{1}{\sqrt{1+{k}^{2}}}$,
故AC=$2\sqrt{{2}^{2}-(\frac{k}{\sqrt{1+{k}^{2}}})^{2}}$=2$\sqrt{\frac{4+3{k}^{2}}{1{+k}^{2}}}$,BD=$2\sqrt{{2}^{2}-{(\frac{1}{\sqrt{1+{k}^{2}}})}^{2}}$=2$\sqrt{\frac{3+4{k}^{2}}{1{+k}^{2}}}$,
故四边形ABCD的面积S=$\frac{1}{2}$AC•BD=2$\frac{\sqrt{(4+3{k}^{2})(3+4{k}^{2})}}{1{+k}^{2}}$,
当k=0时,满足S=2$\frac{\sqrt{(4+3{k}^{2})(3+4{k}^{2})}}{1{+k}^{2}}$,
故S=2$\frac{\sqrt{(4+3{k}^{2})(3+4{k}^{2})}}{1{+k}^{2}}$,
(2)∵S=2$\frac{\sqrt{(4+3{k}^{2})(3+4{k}^{2})}}{1{+k}^{2}}$=2$\sqrt{-(\frac{1}{{k}^{2}+1})^{2}+\frac{1}{{k}^{2}+1}+12}$,
令t=$\frac{1}{{k}^{2}+1}$,则t∈(0,1],S=2$\sqrt{-{t}^{2}+t+12}$,
则当t=$\frac{1}{2}$,即k=1,α=$\frac{π}{4}$时,S取取最大值7
点评 本题考查的知识点是直线与圆的位置关系,函数的最大值,难度中档.

 名校课堂系列答案
名校课堂系列答案| A. | x+y=2 | B. | x+y=1 | C. | x=1或y=1 | D. | x+y=2或x-y=0 |
| A. | 焦点在X轴上的椭圆 | B. | 焦点在Y轴上的椭圆 | ||
| C. | 焦点在X轴上的双曲线 | D. | 焦点在Y轴上的双曲线 |
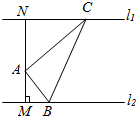 如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则
如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则