题目内容
已知点P在曲线C:y=![]() (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
(Ⅰ)求f(t)的解析式;
(Ⅱ)设数列{an}(n≥1,n∈N)满足a1=1,an=f(![]() )(n≥2),数列{bn}(n≥1,n∈N)满足bn=
)(n≥2),数列{bn}(n≥1,n∈N)满足bn=![]() ,求{an}和{bn}的通项公式;
,求{an}和{bn}的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当1<k<3时,证明不等式:a1+a2+a3+…+an>![]() .
.
答案:
解析:
解析:
解:(Ⅰ)![]() ,(1分)
,(1分)
又点P的坐标为![]() ,∴曲线C在P点的切线斜率为
,∴曲线C在P点的切线斜率为![]() ,
,
则该切线方程为![]() , (2分)
, (2分)
由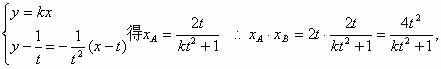
因此,![]() (4分)
(4分)
(Ⅱ)![]() 即
即![]() (6分)
(6分)
①当![]() ; (7分)
; (7分)
②当![]() 为公比等比数列,
为公比等比数列,
![]() (9分)
(9分)
综合①、②得![]() (10分)
(10分)
(Ⅲ)![]()
![]()
![]() (11分)
(11分)
![]()
![]()
![]()
![]()
故不等式![]() (14分)
(14分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
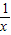 (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.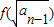 (n≥2),数列{bn}满足bn=
(n≥2),数列{bn}满足bn=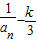 ,求an与bn;
,求an与bn;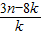 .
.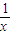 (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.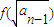 (n≥2),数列{bn}满足bn=
(n≥2),数列{bn}满足bn=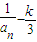 ,求an与bn;
,求an与bn;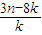 .
.