题目内容
已知点P在曲线C:y=
(x>1)上,曲线C在点P处的切线与函数y=kx(k>0)的图象交于点A,与x轴交于点B,设点P的横坐标为t,点A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(1)求f(t)的解析式;
(2)设数列{an}满足a1=1,an=f(
) (n≥2 且 x∈N*),求数列{an}的通项公式;
(3)在 (2)的条件下,当1<k<3时,证明不等式a1+a2+…+an>
.
| 1 |
| x |
(1)求f(t)的解析式;
(2)设数列{an}满足a1=1,an=f(
| an-1 |
(3)在 (2)的条件下,当1<k<3时,证明不等式a1+a2+…+an>
| 3n-8k |
| k |
分析:(1)由y=
,求出切线方程为y-
=-
(x-t),与y=kx联立得:xA=
,xB=2t,再由f(t)=xA•xB,能求出f(t)的解析式.
(2)由an=f(
)得:an=
,
=
=
•
+
,设bn=
-
,则bn=
-
=
(
-
)=
bn-1,由此导出bn=(1-
)(
)n-1,解得an=
.
(3)因为an-
=
-
=
,由1<k<3,知an-
>
•
,所以a1+a2+…+an-
=(a1-
)+(a2-
)+…+(an-
)=
(1+
+…+
)+8>
+8
=
>0,由此能够证明a1+a2+…+an>
.
| 1 |
| x |
| 1 |
| t |
| 1 |
| t2 |
| 2t |
| kt2+1 |
(2)由an=f(
| an-1 |
| 4an-1 |
| kan-1+1 |
| 1 |
| an |
| kan-1+1 |
| 4an-1 |
| 1 |
| 4 |
| 1 |
| an-1 |
| k |
| 4 |
| 1 |
| an |
| k |
| 3 |
| 1 |
| an |
| k |
| 3 |
| 1 |
| 4 |
| 1 |
| an-1 |
| k |
| 3 |
| 1 |
| 4 |
| k |
| 3 |
| 1 |
| 4 |
| 3•4n-1 |
| k•4n-1+3-k |
(3)因为an-
| 3 |
| k |
| 3•4n-1 |
| k•4n-1+3-k |
| 3 |
| k |
| 3k-9 |
| k2•4n-1+k(3-k) |
| 3 |
| k |
| 3k-9 |
| k2 |
| 1 |
| 4n-1 |
| 3n-8k |
| k |
| 3 |
| k |
| 3 |
| k |
| 3 |
| k |
| 3k-9 |
| k2 |
| 1 |
| 4 |
| 1 |
| 4n-1 |
| 4(k-3) |
| k2 |
=
| 4(2k+3)(k-1) |
| k2 |
| 3n-8k |
| k |
解答:解:(1)∵y=
,
∴y′=-
,
∴切线方程为y-
=-
(x-t),
与y=kx联立得:xA=
,令y=0,得:xB=2t,
∵f(t)=xA•xB,
∴f(t)=
(k>0,t>1).
(2)由an=f(
)得:an=
,
=
=
•
+
,
设bn=
-
,
则bn=
-
=
(
-
)=
bn-1,
∵a1=1,
∴①当k=3时,b1=
-1=0,
∴{bn}是以0为首项的常数数列,
∴an=1.
②当k≠3时,{bn}是以1-
为首项,
为公比的等比数列,
∴bn=(1-
)(
)n-1,
解得an=
,
由①②,得an=
.
(3)∵an-
=
-
=
=
,
∵1<k<3,
∴an-
>
•
,
∴a1+a2+…+an-
=(a1-
)+(a2-
)+…+(an-
)
=
(1+
+…+
)+8
=
[1-(
)n]+8
>
+8
=
,
∵1<k<3,
∴
>0.
∴a1+a2+…+an>
.
| 1 |
| x |
∴y′=-
| 1 |
| x2 |
∴切线方程为y-
| 1 |
| t |
| 1 |
| t2 |
与y=kx联立得:xA=
| 2t |
| kt2+1 |
∵f(t)=xA•xB,
∴f(t)=
| 4t2 |
| kt2+1 |
(2)由an=f(
| an-1 |
| 4an-1 |
| kan-1+1 |
| 1 |
| an |
| kan-1+1 |
| 4an-1 |
| 1 |
| 4 |
| 1 |
| an-1 |
| k |
| 4 |
设bn=
| 1 |
| an |
| k |
| 3 |
则bn=
| 1 |
| an |
| k |
| 3 |
| 1 |
| 4 |
| 1 |
| an-1 |
| k |
| 3 |
| 1 |
| 4 |
∵a1=1,
∴①当k=3时,b1=
| 1 |
| a1 |
∴{bn}是以0为首项的常数数列,
∴an=1.
②当k≠3时,{bn}是以1-
| k |
| 3 |
| 1 |
| 4 |
∴bn=(1-
| k |
| 3 |
| 1 |
| 4 |
解得an=
| 3•4n-1 |
| k•4n-1+3-k |
由①②,得an=
| 3•4n-1 |
| k•4n-1+3-k |
(3)∵an-
| 3 |
| k |
| 3•4n-1 |
| k•4n-1+3-k |
| 3 |
| k |
=
| 3k-9 |
| k(k•4n-1+3-k) |
=
| 3k-9 |
| k2•4n-1+k(3-k) |
∵1<k<3,
∴an-
| 3 |
| k |
| 3k-9 |
| k2 |
| 1 |
| 4n-1 |
∴a1+a2+…+an-
| 3n-8k |
| k |
=(a1-
| 3 |
| k |
| 3 |
| k |
| 3 |
| k |
=
| 3k-9 |
| k2 |
| 1 |
| 4 |
| 1 |
| 4n-1 |
=
| 4(k-3) |
| k2 |
| 1 |
| 4 |
>
| 4(k-3) |
| k2 |
=
| 4(2k+3)(k-1) |
| k2 |
∵1<k<3,
∴
| 4(2k+3)(k-1) |
| k2 |
∴a1+a2+…+an>
| 3n-8k |
| k |
点评:本题考查数列与不等式的综合,综合性强,难度大,容易出错.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
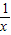 (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.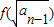 (n≥2),数列{bn}满足bn=
(n≥2),数列{bn}满足bn=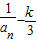 ,求an与bn;
,求an与bn;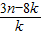 .
.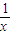 (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.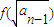 (n≥2),数列{bn}满足bn=
(n≥2),数列{bn}满足bn=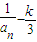 ,求an与bn;
,求an与bn;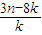 .
.