题目内容
11．在复平面内，复数i2（1-i）对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 首先将分式化简为a+bi的形式，然后找到对应的坐标，得到选项．
解答 解：复数i2（1-i）=-1（1-i）=-1+i；对应的点为（-1，1），所以复数i2（1-i）对应的点在第二象限；
故选：B．
点评 本题考查了复数的运算以及复数的几何意义；属于基础题．
练习册系列答案
相关题目
1．斜率为2的直线L经过抛物线y2=2px（p＞0）的焦点F，且交抛物线与A、B两点，若AB的中点到抛物线准线的距离1，则P的值为（ ）
| A． | 1 | B． | $\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{5}$ |
19．如图，在正方体ABCD-A1B1C1D1中，直线A1B与直线C1D1所成的角为（ ）
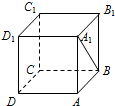
| A． | 90° | B． | 60° | C． | 45° | D． | 30° |
6．已知函数f（x）=cos（2x+φ）（φ为常数）为奇函数，那么cosφ=（ ）
| A． | -$\frac{{\sqrt{2}}}{2}$ | B． | 0 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | 1 |
16．在△ABC中，若a=3，c=$\sqrt{3}，∠A=\frac{π}{3}$，则b=（ ）
| A． | 4 | B． | 6 | C． | $2\sqrt{3}$ | D． | $\sqrt{6}$ |
如图，在直角坐标系中，曲线段AB是函数y=1-x2图象的一部分，P为曲线段AB上异于点A，B一个动点，PM丄x轴，垂足为M，PN丄y轴，垂足为N．