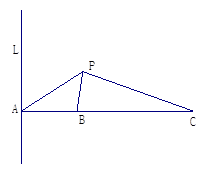
题目内容
已知直线 过椭圆E:
过椭圆E: 的右焦点
的右焦点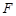 ,且与E相交于
,且与E相交于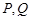 两点.
两点.
(1)设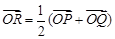 (
( 为原点),求点
为原点),求点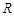 的轨迹方程;
的轨迹方程;
(2)若直线 的倾斜角为
的倾斜角为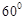 ,求
,求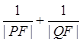 的值.
的值.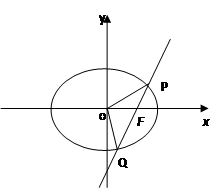
 过椭圆E:
过椭圆E: 的右焦点
的右焦点 ,且与E相交于
,且与E相交于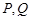 两点.
两点.(1)设
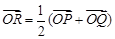 (
( 为原点),求点
为原点),求点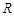 的轨迹方程;
的轨迹方程;(2)若直线
 的倾斜角为
的倾斜角为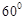 ,求
,求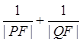 的值.
的值.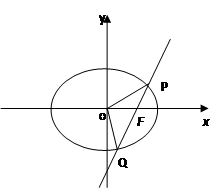
(1) ;(2)
;(2)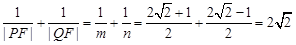
 ;(2)
;(2)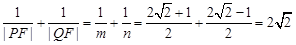
第一问中,利用向量的表达式,坐标的手段得到所求点的轨迹方程。
当直线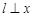 轴时,直线
轴时,直线 的方程是:
的方程是: ,根据对称性可知
,根据对称性可知
当直线 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为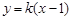
代入E有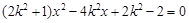
 ;
; 
第二问中,在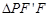 中
中 设
设 ,则
,则
由余弦定理得

同理,在 ,设
,设 ,则
,则
也由余弦定理得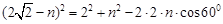

然后可得。
解:(1)设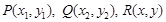
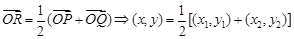

由 ,易得右焦点
,易得右焦点 -(2分)
-(2分)
当直线 轴时,直线
轴时,直线 的方程是:
的方程是: ,根据对称性可知
,根据对称性可知
当直线 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为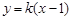
代入E有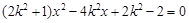
 ;
;  ---(5分)
---(5分)
于是
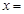
 ;
; 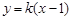
消去参数 得
得 而
而 也适上式,故R的轨迹方程是
也适上式,故R的轨迹方程是 ----(8分)
----(8分)
(2)设椭圆另一个焦点为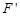 ,
,
在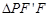 中
中 设
设 ,则
,则
由余弦定理得

同理,在 ,设
,设 ,则
,则
也由余弦定理得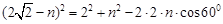

于是 ………12分
………12分
当直线
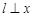 轴时,直线
轴时,直线 的方程是:
的方程是: ,根据对称性可知
,根据对称性可知
当直线
 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为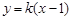
代入E有
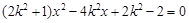
 ;
; 
第二问中,在
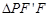 中
中 设
设 ,则
,则
由余弦定理得


同理,在
 ,设
,设 ,则
,则
也由余弦定理得
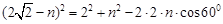

然后可得。
解:(1)设
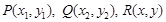
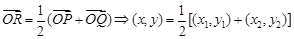

由
 ,易得右焦点
,易得右焦点 -(2分)
-(2分)当直线
 轴时,直线
轴时,直线 的方程是:
的方程是: ,根据对称性可知
,根据对称性可知
当直线
 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为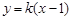
代入E有
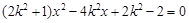
 ;
;  ---(5分)
---(5分)于是

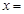
 ;
; 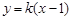
消去参数
 得
得 而
而 也适上式,故R的轨迹方程是
也适上式,故R的轨迹方程是 ----(8分)
----(8分)(2)设椭圆另一个焦点为
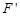 ,
,在
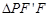 中
中 设
设 ,则
,则
由余弦定理得


同理,在
 ,设
,设 ,则
,则
也由余弦定理得
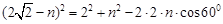

于是
 ………12分
………12分 
练习册系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为 ,则
,则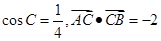 且
且 ,则
,则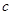 等于( )
等于( )
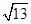
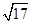
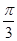 ,且△ABC的面积为
,且△ABC的面积为 ,则AC的长为_____.
,则AC的长为_____.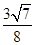
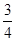
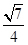
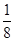
 中,角
中,角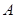 、
、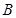 、
、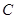 的对边分别是
的对边分别是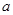 ,
,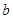 ,
,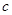 ,已知
,已知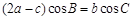 .
.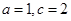 ,求
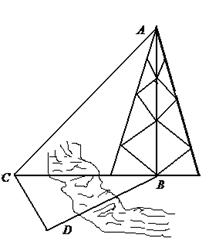
,求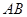 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点 .现测得
.现测得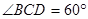
 ,并在点
,并在点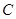 测得塔顶
测得塔顶 的仰角为
的仰角为 , 求塔高
, 求塔高 ,
, )
)
 方向300
方向300 的海面P处,并以
的海面P处,并以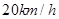 的速度向西偏北
的速度向西偏北 方向移动。台风侵袭的范围为圆形区域,当前半径为60
方向移动。台风侵袭的范围为圆形区域,当前半径为60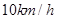 的速度不断增大,问几时后该城市开始受到台风的侵袭?
的速度不断增大,问几时后该城市开始受到台风的侵袭?
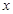 km,用
km,用 中,若
中,若 ,则
,则 ( )
( )


