题目内容
【题目】已知有相同焦点
、
的椭圆和双曲线交于点
，
，椭圆和双曲线的离心率分别是
、
，那么
__________（点
为坐标原点）．
【答案】
【解析】
设出椭圆的长半轴，双曲线的实半轴，它们的半焦距，利用椭圆的和双曲线的定义可得焦半径，写出两个曲线的离心率，即可得到结果．
设椭圆的长半轴是a1，双曲线的实半轴是a2，它们的半焦距是c
并设|PF1|＝m，|PF2|＝n，m＞n，根据椭圆的和双曲线的定义可得m+n＝2a1，m﹣n＝2a2，
解得m＝a1+a2，n＝a1﹣a2，
∵
，∴PF1⊥PF2，
由勾股定理得|PF1|2+|PF2|2＝|F1F2|2
∴（a1+a2）2+（a1﹣a2）2＝（2c）2
化简可得a12+a22＝2c2
∴
2
故答案为：2
练习册系列答案
阳光课堂同步练习系列答案
相关题目
【题目】某市工业部门计划对所辖中小型企业推行节能降耗技术改造，下面是对所辖企业是否支持技术改造进行的问卷调查的结果：
支持 | 不支持 | 合计 | |
中型企业 | 40 | ||
小型企业 | 240 | ||
合计 | 560 |
已知从这560家企业中随机抽取1家，抽到支持技术改造的企业的概率为
.
（1）能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关？
（2）从上述支持节能降耗的中小企业中按分层抽样的方法抽出12家企业，然后从这12家企业选出9家进行奖励，分别奖励中型企业50万元，小型企业10万元.设
为所发奖励的金额.
求的分布列和期望.
附：
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【题目】假设关于某种设备的使用年限
(年)与所支出的维修费用
(万元)有如下统计：
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
. 
， 
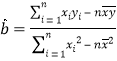(1)求
， 
；
(2)与具有线性相关关系，求出线性回归方程；
(3)估计使用年限为10年时，维修费用约是多少？