Question

【题目】已知椭圆的右焦点为F.

（1）求点F的坐标和椭圆C的离心率；

（2）直线过点F，且与椭圆C交于P，Q两点，如果点P关于x轴的对称点为，判断直线是否经过x轴上的定点，如果经过，求出该定点坐标；如果不经过，说明理由.

Answer 1

【答案】（1）焦点，离心率（2）是过x轴上的定点；定点

【解析】

（1）由椭圆的标准方程即可得出；

（2）直线过点F，可得，代入椭圆的标准方程可得：.（依题意）.设，，可得根与系数的关系，点P关于x轴的对称点为，则.可得直线的方程可以为，令，，把根与系数的关系代入化简即可得出.

（1）椭圆，

，解得，

焦点，离心率.

（2）直线过点F，

，.

由，得.（依题意）.

设，，

则，.

点P关于x轴的对称点为，则.

直线的方程可以设为，

令，

.

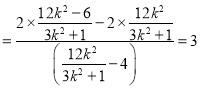直线过x轴上定点.