题目内容
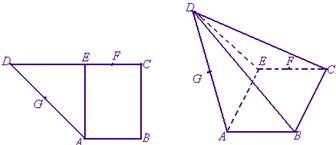 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+| 2 |
(Ⅰ)求证:FG∥平面BCD;
(Ⅱ)求异面直线GF与BD所成角的余弦值;
(Ⅲ)求二面角A-BD-C的大小.
分析:(I)取AB中点H,连接GH,FH,利用三角形中位线定理,我们易判断GH∥BD,FH∥BC,进而根据面面平行的判定定理,得到面FHG∥面BCD,结合面面平行的性质,即可得到结论.
(Ⅱ)延长CE,过D作DO垂直于直线CE的延长线于O,可得:DO⊥平面ABCE,根据题意可得:DEO=45°,再过O作OM⊥OC,进而建立空间直角坐标系利用空间向量的有关知识求出线线角.
(Ⅲ)分别求出两个平面的法向量,利用空间向量的有关知识求出两个向量的夹角,进而转化为两个平面的平面角.
(Ⅱ)延长CE,过D作DO垂直于直线CE的延长线于O,可得:DO⊥平面ABCE,根据题意可得:DEO=45°,再过O作OM⊥OC,进而建立空间直角坐标系利用空间向量的有关知识求出线线角.
(Ⅲ)分别求出两个平面的法向量,利用空间向量的有关知识求出两个向量的夹角,进而转化为两个平面的平面角.
解答:解:(Ⅰ)取AB中点为H,连接GH,FH,又G为AD的中点,
∴GH∥BD.
又因为GH?平面BCD,BD?平面BCD,
∴GH∥平面BCD
同理可证FH∥BC,FH∥平面BCD,
所以面FHG∥面BCD,
又∵GF?平面FGH,
∴FG∥平面BCD…(3分)
(Ⅱ)延长CE,过D作DO垂直于直线CE的延长线于O,易证DO⊥平面ABCE
又∵AE⊥EC,AE⊥DE,二面角D-AE-C的平面角为135°
∴∠DEO=45°∵DE=
∴OE=1,DO=1
过O作OM⊥OC,
所以以O为原点,以OM,OC,OD所在的直线分别为x轴,y轴,z轴,建立如图所示的直角坐标系.
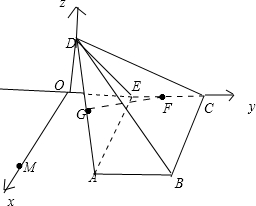
则D(0,0,1),A(2,1,0),E(0,1,0),C(0,2,0),B(2,2,0),H(2,
,0),G(1,
,
),F(0,
,0),
所以
=(-1,1,-
),
=(-2,-2,1),
所以cos<
,
>=
=-
所以异面直线GF与BD所成的角的余弦值为
…(8分)
(Ⅲ)
=(2,1,-1),
=(2,2,-1),
=(0,2,-1)
设平面ABD的法向量为
1=(x,y,z),
则
,即
∴取
=(x,0,2x)
设平面BDC的法向量为
2=(a,b,c),
则
,即
∴
=(0,b,2b)
∴cos<
,
>=
∴二面角A-BD-C大小为π-arccos
.…(12分)
∴GH∥BD.
又因为GH?平面BCD,BD?平面BCD,
∴GH∥平面BCD
同理可证FH∥BC,FH∥平面BCD,
所以面FHG∥面BCD,
又∵GF?平面FGH,
∴FG∥平面BCD…(3分)
(Ⅱ)延长CE,过D作DO垂直于直线CE的延长线于O,易证DO⊥平面ABCE
又∵AE⊥EC,AE⊥DE,二面角D-AE-C的平面角为135°
∴∠DEO=45°∵DE=
| 2 |
∴OE=1,DO=1
过O作OM⊥OC,
所以以O为原点,以OM,OC,OD所在的直线分别为x轴,y轴,z轴,建立如图所示的直角坐标系.

则D(0,0,1),A(2,1,0),E(0,1,0),C(0,2,0),B(2,2,0),H(2,
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以
| GF |
| 1 |
| 2 |
| BD |
所以cos<
| GF |
| BD |
| ||||
|
|
| 1 |
| 9 |
所以异面直线GF与BD所成的角的余弦值为
| 1 |
| 9 |
(Ⅲ)
| DA |
| DB |
| DC |
设平面ABD的法向量为
| n |
则
|
|
∴取
| n1 |
设平面BDC的法向量为
| n |
则
|
|
∴
| n2 |
∴cos<
| n1 |
| n2 |
| 4 |
| 5 |
∴二面角A-BD-C大小为π-arccos
| 4 |
| 5 |
点评:本题考查用线面平行的判定定理证明线面平行,以及求二面角的平面角与异面直线的夹角,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键,也可以根据几何体的结构特征建立空间直角坐标系利用向量的有关知识解决空间角等问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则