题目内容
设函数f(x)=cos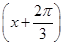 +2cos2
+2cos2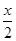 ,x∈R.
,x∈R.
(1)求f(x)的值域;
(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若f(B)=1,b=1,c=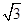 ,求a的值.
,求a的值.
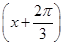 +2cos2
+2cos2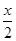 ,x∈R.
,x∈R.(1)求f(x)的值域;
(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若f(B)=1,b=1,c=
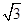 ,求a的值.
,求a的值.(1)[0,2] (2)1或2
(1)f(x)=cos xcos 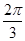 -sin xsin
-sin xsin 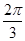 +cos x+1
+cos x+1
=-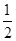 cos x-
cos x-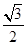 sin x+cos x+1
sin x+cos x+1
=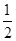 cos x-
cos x-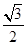 sin x+1
sin x+1
=sin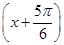 +1,
+1,
因此f(x)的值域为[0,2].
(2)由f(B)=1得sin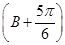 +1=1,
+1=1,
即sin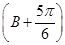 =0,又因0<B<π,
=0,又因0<B<π,
故B=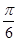 .
.
方法一 由余弦定理b2=a2+c2-2accos B,
得a2-3a+2=0,解得a=1或2.
方法二 由正弦定理 =
=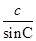 ,得
,得
sin C=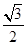 ,C=
,C= 或
或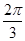 .
.
当C= 时,A=
时,A=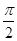 ,
,
从而a=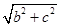 =2;
=2;
当C=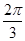 时,A=
时,A=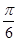 ,
,
又B=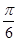 ,
,
从而a=b=1.
故a的值为1或2.
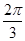 -sin xsin
-sin xsin 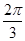 +cos x+1
+cos x+1=-
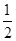 cos x-
cos x-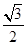 sin x+cos x+1
sin x+cos x+1=
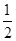 cos x-
cos x-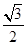 sin x+1
sin x+1=sin
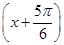 +1,
+1,因此f(x)的值域为[0,2].
(2)由f(B)=1得sin
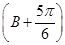 +1=1,
+1=1,即sin
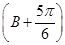 =0,又因0<B<π,
=0,又因0<B<π,故B=
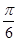 .
.方法一 由余弦定理b2=a2+c2-2accos B,
得a2-3a+2=0,解得a=1或2.
方法二 由正弦定理
 =
=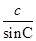 ,得
,得sin C=
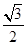 ,C=
,C= 或
或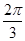 .
.当C=
 时,A=
时,A=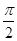 ,
,从而a=
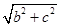 =2;
=2;当C=
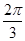 时,A=
时,A=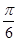 ,
,又B=
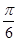 ,
,从而a=b=1.
故a的值为1或2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
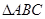 中,角
中,角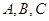 的对边分别为
的对边分别为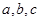 ,已知
,已知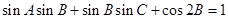 .
.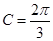
 ,求
,求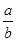 的值.
的值.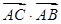 =4,求△ABC的面积S.
=4,求△ABC的面积S. ,AC=2
,AC=2 ,cosC=
,cosC= .
.
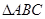 中,内角
中,内角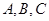 的对边分别为
的对边分别为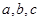 ,若
,若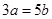 ,且
,且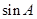 是
是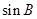 与
与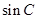 的等差中项,则角
的等差中项,则角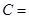 _________.
_________.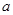 、
、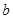 、
、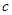 分别是
分别是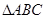 的三个内角
的三个内角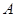 、
、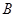 、
、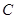 的对边.
的对边.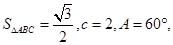 求
求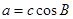 ,且
,且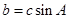 ,试判断
,试判断 的三边分别为
的三边分别为 ,
, ,
, ,且
,且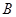 =45°,
=45°, =2,则
=2,则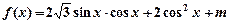 在区间
在区间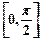 上的最大值为2
上的最大值为2 .
.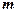 的值;
的值;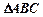 中的角
中的角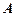 ,
,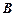 ,
,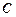 所对的边是
所对的边是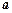 ,
,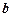 ,
,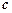 ,若
,若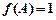
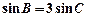 ,
,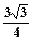 . 求边长
. 求边长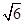 ,∠B=2∠A,
,∠B=2∠A,