Question

【题目】设函数， ．

（1）解方程．

（2）令，求的值．

（3）若是定义在上的奇函数，且对任意恒成立，求实数k的取值范围．

Answer 1

【答案】(1)2.(2)1009.(3) .

【解析】

（1）将题中的条件代入得，将视作为整体，先求出的值，从而得出的值；

（2）根据题意发现规律，由此规律解得结果；

（3）根据题意首先求出的值，研究出函数的单调性，将题中的不等式转化为恒成立问题，分离变量构造函数，求解新函数最值，从而得出结果.

解：（1）因为

即 ，

即 ，

解得 或 （舍）

故．

（2）∵

，

=1009.

（3）∵是实数集上的奇函数，

∴，

∴，

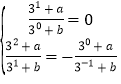解得， ，

∴，

即，

设，

则

因为，，

所以

所以，

所以在上单调递增，

由

得，

又∵是上的奇函数，

∴，

又∵在上单调递增，

∴，

即对任意的都成立，

即对任意都成立，

又∵，当且仅当，即时取“=”，

∴.

故实数的取值范围是．