题目内容
【题目】设函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)求![]() 的零点个数;
的零点个数;
(Ⅲ)证明:曲线![]() 没有经过原点的切线.
没有经过原点的切线.
【答案】(Ⅰ)![]() 时,
时,![]() 在
在![]() 内单调递增;
内单调递增;![]() 时,
时,![]() ,
,![]() ,
,![]() 在区间
在区间![]() 及
及![]() 内单调递增,在
内单调递增,在![]() 内单调递减;(Ⅱ)有且仅有一个零点;(Ⅲ)证明见解析.
内单调递减;(Ⅱ)有且仅有一个零点;(Ⅲ)证明见解析.
【解析】
试题分析:(Ⅰ)本小题要求单调区间,可先求定义域为![]() ,再求出导数
,再求出导数![]() ,研究
,研究![]() 的根的情况,从而得出
的根的情况,从而得出![]() 的解集,得单调区间;(Ⅱ)函数
的解集,得单调区间;(Ⅱ)函数![]() 的零点个数,可利用(Ⅰ)的单调性证明,如当
的零点个数,可利用(Ⅰ)的单调性证明,如当![]() 时,
时,![]() 在
在![]() 内单调递增,最多只有1个零点,如能说明函数有正有负,则一定有一个零点;当
内单调递增,最多只有1个零点,如能说明函数有正有负,则一定有一个零点;当![]() 时,
时,![]() 在
在![]() 及
及![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,![]() 是
是![]() 的根,要讨论
的根,要讨论![]() 的正负,从而确定零点个数;(Ⅲ)用反证,假设曲线
的正负,从而确定零点个数;(Ⅲ)用反证,假设曲线![]() 在点
在点![]() 处的切线经过原点,则有
处的切线经过原点,则有![]() ,化简得
,化简得![]() .下面只要证明此方程无解即可,可求函数
.下面只要证明此方程无解即可,可求函数![]()
![]() 的最小值,证得结论.
的最小值,证得结论.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 内单调递增.
内单调递增.
当![]() ,即
,即![]() 时,由
时,由![]() 解得,
解得,
![]() ,
,![]() ,且
,且![]() ,
,
在区间![]() 及
及![]() 内,
内,![]() ,在
,在![]() 内,
内,![]() ,
,
∴![]() 在区间
在区间![]() 及
及![]() 内单调递增,在
内单调递增,在![]() 内单调递减.
内单调递减.
(Ⅱ)由(Ⅰ)可知,当![]() 时,
时,![]() 在
在![]() 内单调递增,
内单调递增,
∴![]() 最多只有一个零点.
最多只有一个零点.
又∵![]() ,∴当
,∴当![]() 且
且![]() 时,
时,![]() ;
;
当![]() 且
且![]() 时,
时,![]() ,故
,故![]() 有且仅有一个零点.
有且仅有一个零点.
当![]() 时,∵
时,∵![]() 在
在![]() 及
及![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,
且![]() ,
,
![]() ,
,
而![]() ,
,
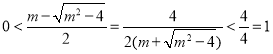 (∵
(∵![]() ),
),
∴![]() ,由此知
,由此知![]() ,
,
又∵当![]() 且
且![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内有且仅有一个零点.
内有且仅有一个零点.
综上所述,当![]() 时,
时,![]() 有且仅有一个零点.
有且仅有一个零点.
(Ⅲ)假设曲线![]() 在点
在点![]() 处的切线经过原点,
处的切线经过原点,
则有![]() ,即
,即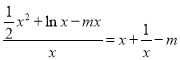 ,
,
化简得:![]() .(*)
.(*)
记![]() ,则
,则![]() ,
,
令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 是
是![]() 的最小值,即当
的最小值,即当![]() 时,
时,![]() .
.
由此说明方程(*)无解,∴曲线![]() 没有经过原点的切线.
没有经过原点的切线.

练习册系列答案
相关题目
