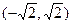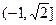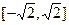题目内容
在△ABC中,A为最小角,C为最大角,已知cos(2A+C)=-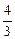 ,sinB=
,sinB=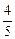 ,则cos2(B+C)=__________.
,则cos2(B+C)=__________.
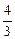 ,sinB=
,sinB=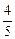 ,则cos2(B+C)=__________.
,则cos2(B+C)=__________.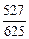
∵A为最小角∴2A+C=A+A+C<A+B+C=180°.
∵cos(2A+C)=-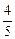 ,∴sin(2A+C)=
,∴sin(2A+C)=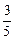 .
.
∵C为最大角,∴B为锐角,又sinB=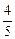 . 故cosB=
. 故cosB=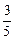 .
.
即sin(A+C)=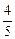 ,cos(A+C)=-
,cos(A+C)=-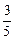 .
.
∵cos(B+C)=-cosA=-cos[(2A+C)-(A+C)]=-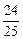 ,
,
∴cos2(B+C)=2cos2(B+C)-1=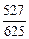 .
.
∵cos(2A+C)=-
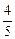 ,∴sin(2A+C)=
,∴sin(2A+C)=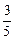 .
. ∵C为最大角,∴B为锐角,又sinB=
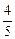 . 故cosB=
. 故cosB=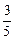 .
. 即sin(A+C)=
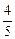 ,cos(A+C)=-
,cos(A+C)=-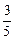 .
. ∵cos(B+C)=-cosA=-cos[(2A+C)-(A+C)]=-
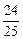 ,
,∴cos2(B+C)=2cos2(B+C)-1=
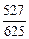 .
.
练习册系列答案
相关题目
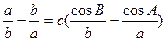
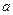 、
、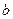 、
、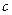 ,且
,且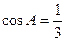 .
.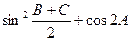 的值;
的值;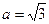 ,求
,求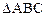 面积的最大值.
面积的最大值.
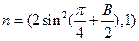 ,m⊥n,
,m⊥n,
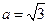 ,b=1,求c的值.
,b=1,求c的值.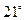 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成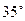 夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
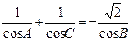 ,求cos
,求cos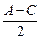 的值.
的值. 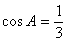 .
.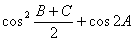 的值;
的值;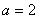 ,
,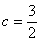 ,求∠C和ΔABC的面积.
,求∠C和ΔABC的面积.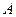 为△ABC的内角,则
为△ABC的内角,则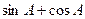 的取值范围是( )
的取值范围是( )