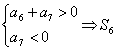Question

设等差数列{a_n}的前n项和为S_n，已知a₃=12，S₁₂>0，S₁₃<0；

(1)求公差d的取值范围；

(2)指出S₁，S₂，…，S₁₂中那一个值最大，说明理由。

 

Answer 1

答案：
解析：

（1）， 由a3=12得a1=12－2d代入上式，得： ； （2）由d<0， ∴a1>a2>a3>…>a12>a13。 ∴1≤n≤12中必存在自然数n，使an>0，an+l<0， 则Sn就是S1，S2，S3，…，S12中的最大值。 ∵S12=6(a6+a7)>0，S13=13a7<0， ∴是这些和中的最大值。