题目内容
设P是 所在平面上一点,且满足
所在平面上一点,且满足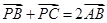 ,若
,若 的面积为1,则
的面积为1,则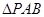 的面积为( )
的面积为( )
A.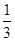 | B. | C.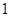 | D.2 |
B
解析试题分析:取BC的中点D,则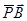 +
+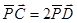
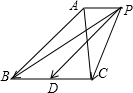
∵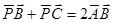 ∴
∴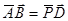
∴四边形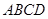 是平行四边形
是平行四边形
∵ 的中点
的中点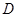 ,∴
,∴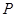 到
到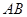 的距离为
的距离为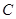 到
到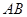 距离的一半
距离的一半
∵ 的面积为1,∴△
的面积为1,∴△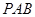 的面积为
的面积为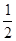
故选B.
考点:向量在几何中的应用;三角形的面积公式.
点评:本题考查向量的运算,考查三角形面积的计算,确定P到AB的距离为C到AB距离的一半是关键.

练习册系列答案
相关题目
下列各组向量中,可以作为基底的是 ( )
A. | B.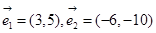 |
C.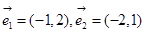 | D.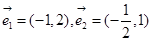 |
已知向量 ,
, 满足|
满足| |=2,|
|=2,| |=3,|2
|=3,|2 +
+ |=
|=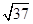 ,则
,则 与
与 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.90° |
已知向量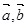 满足
满足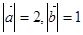 ,其夹角为
,其夹角为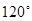 ,若对任意向量
,若对任意向量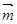 ,总有
,总有 ,则
,则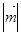 的最大值与最小值之差为
的最大值与最小值之差为
| A.1 | B.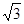 | C.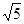 | D.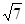 |
已知 ,若向量
,若向量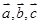 共面,
共面,
则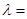 ( )
( )
A.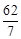 | B.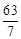 | C.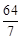 | D.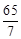 |
已知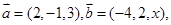
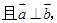 则
则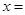 ( )
( )
A.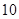 | B.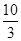 | C.3 | D.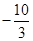 |
对任意两个非零的平面向量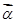 和
和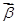 ,定义
,定义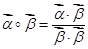 .若平面向量
.若平面向量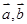 满足
满足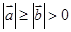 ,
,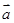 与
与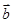 的夹角
的夹角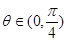 ,且
,且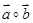 和
和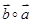 都在集合
都在集合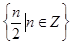 中,则
中,则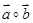 =
=
A.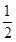 | B.1 | C.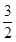 | D.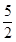 |
向量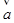 = (cosθ, sinθ),
= (cosθ, sinθ),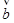 = (
= (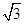 , 1),则
, 1),则 的最大值为( )
的最大值为( )
| A.3 | B.4 | C.5 | D.6 |
已知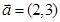 ,
,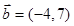 ,则向量
,则向量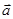 在
在 方向上设射影的数量为( )
方向上设射影的数量为( )
A.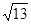 | B.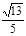 | C.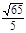 | D.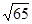 |