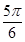题目内容
已知向量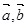 满足
满足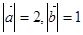 ,其夹角为
,其夹角为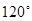 ,若对任意向量
,若对任意向量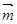 ,总有
,总有 ,则
,则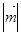 的最大值与最小值之差为
的最大值与最小值之差为
| A.1 | B.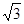 | C.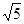 | D.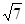 |
B
解析试题分析:根据题意设出向量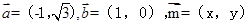 有
有 得到及向量的数量积的坐标表示整理出x,y的关系,结合圆的性质及几何意义可求。即可知
得到及向量的数量积的坐标表示整理出x,y的关系,结合圆的性质及几何意义可求。即可知
故可知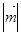 的最大值为
的最大值为 ,那么可知最大值与最小值差
,那么可知最大值与最小值差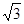 ,选B.
,选B.
考点:向量的数量积与向量的模的最值
点评:本题考查的知识点是两向量的和与差的模的最值,及向量加减法的几何意义,其中根据已知条件,判断出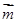
满足的关系,是解答本题的关键.

练习册系列答案
相关题目
在下列各组向量中,能作为表示它们所在平面内所有向量的基底的是( )
A.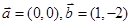 | B.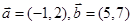 |
C.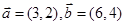 | D.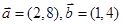 |
设两个向量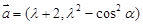 和
和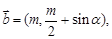 其中
其中 为实数.若
为实数.若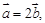 则
则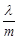 的取值范围是 ( )
的取值范围是 ( )
A.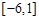 | B.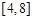 | C. | D. |
若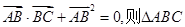 是 ( )
是 ( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.等腰直角三角形 |
在四边形ABCD中,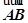 =
=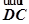 ,且
,且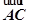 ·
·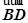 =0,则四边形ABCD是( )
=0,则四边形ABCD是( )
| A.矩形 | B.菱形 | C.直角梯形 | D.等腰梯形 |
设P是 所在平面上一点,且满足
所在平面上一点,且满足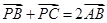 ,若
,若 的面积为1,则
的面积为1,则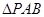 的面积为( )
的面积为( )
A.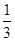 | B. | C.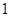 | D.2 |
在△ABC中,∠C=90°, =(k,1),
=(k,1), 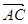 =(2,3),则k的值是( )
=(2,3),则k的值是( )
| A.5 | B.-5 | C. | D.- 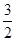 |
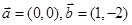
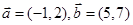
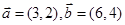
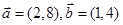
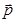 =(sinA,b+c),
=(sinA,b+c),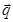 =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足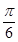 B.
B.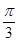 C.
C.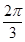 D.
D.