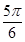题目内容
对任意两个非零的平面向量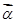 和
和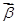 ,定义
,定义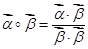 .若平面向量
.若平面向量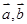 满足
满足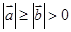 ,
,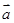 与
与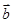 的夹角
的夹角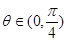 ,且
,且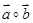 和
和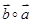 都在集合
都在集合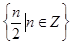 中,则
中,则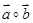 =
=
A.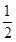 | B.1 | C.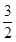 | D.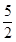 |
C
解析试题分析: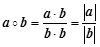
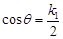 ,
,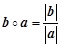
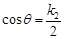 ,两式相乘,可得
,两式相乘,可得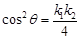 .因为
.因为 ,所以
,所以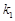 、
、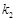 都是正整数,于是
都是正整数,于是 ,即
,即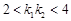 ,所以
,所以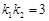 .而
.而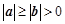 ,所以
,所以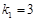 ,
,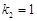 ,于是
,于是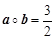 .
.
考点:向量的综合应用。
点评:做此题的关键是迅速理解新定义,然后根据新定义来做题。对学生的理解能力要求较高。此题难度较大,我们要认真分析,仔细解答。

练习册系列答案
相关题目
已知平行四边形ABCD的三个顶点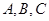 的坐标分别是
的坐标分别是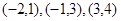 ,则向量
,则向量 的坐标是( )
的坐标是( )
A.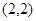 | B.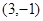 | C.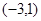 | D.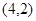 |
设P是 所在平面上一点,且满足
所在平面上一点,且满足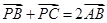 ,若
,若 的面积为1,则
的面积为1,则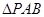 的面积为( )
的面积为( )
A.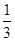 | B. | C.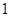 | D.2 |
如图所示,点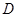 是△
是△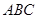 的边
的边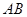 上的中点,则向量
上的中点,则向量 ( )
( )
A.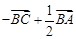 | B.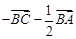 | C.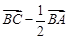 | D.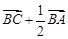 |
向量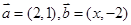 ,若
,若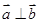 ,则
,则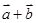 = ( )
= ( )
| A.(3,-1) | B.(-3,1) | C.(-2,-1) | D.(2 ,1) |
设向量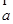 =(1,-3),
=(1,-3), 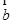 =(-2,4),
=(-2,4), 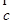 =(-1,-2),若表示向量4
=(-1,-2),若表示向量4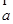 ,4
,4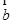 -2
-2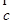 ,2(
,2(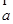 -
-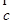 ),
),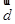 的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量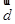 为( )
为( )
| A.(2,6) | B.(-2,6) | C.(2,-6) | D.(-2,-6) |
平面向量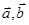 ,已知
,已知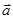 =(4,3),
=(4,3),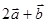 =(3,18),则
=(3,18),则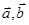 夹角的余弦值等于
夹角的余弦值等于
A.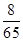 | B.-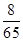 | C.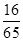 | D.-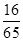 |
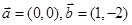
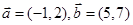
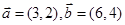
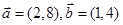
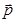 =(sinA,b+c),
=(sinA,b+c),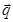 =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足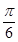 B.
B.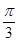 C.
C.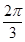 D.
D.